09/11/2021
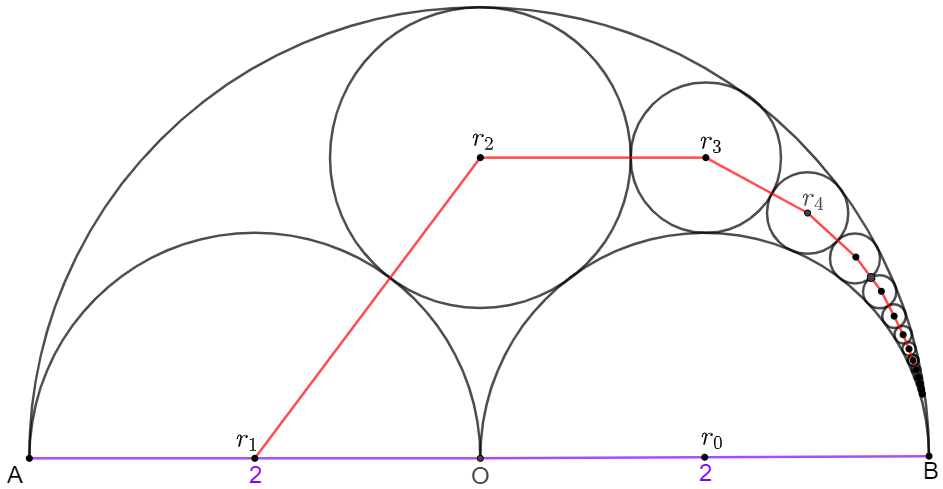
Calculate the total length of segments in red color.
Solve 1:
Using Descartes’s Theorem,
Four circles centered at $O, r_0, r_1, r_2$ are tangent to each other, so
$2(\dfrac{1}{2^2}+\dfrac{1}{1}+\dfrac{1}{1}+\dfrac{1}{r_2^2})=(-\dfrac{1}{2}+\dfrac{1}{1}+\dfrac{1}{1}+\dfrac{1}{r_2})^2 \implies r_2=\dfrac{2}{3}$
Four circles centered at $O, r_0, r_2, r_3$ are tangent to each other, so
$2(\dfrac{1}{2^2}+\dfrac{1}{1}+\dfrac{3^2}{2^2}+\dfrac{1}{r_3^2})=(-\dfrac{1}{2}+\dfrac{1}{1}+\dfrac{3}{2}+\dfrac{1}{r_3^2})^2 \implies r_3=\dfrac{1}{3}$
And Four circles centered at $O, r_0, r_{n-1},r_{n}$ are tangent to each other, so
$2(\dfrac{1}{2^2}+\dfrac{1}{1}+\dfrac{1}{r_{n-1}^2}+\dfrac{1}{r_n^2})=(-\dfrac{1}{2}+\dfrac{1}{1}+\dfrac{1}{r_{n-1}}+\dfrac{1}{r_n})^2$
Four circles centered at $O, r_0, r_{n-2}, r_{n-1}$ are tangent to each other, so
$2(\dfrac{1}{2^2}+\dfrac{1}{1}+\dfrac{1}{r_{n-2}^2}+\dfrac{1}{r_{n-1}^2})=(-\dfrac{1}{2}+\dfrac{1}{1}+\dfrac{1}{r_{n-2}}+\dfrac{1}{r_{n-1}})^2$
In above two equations, take $c_{n-1}=\dfrac{1}{r_{n-1}}$ as known value,
and take $c_{n-2}=\dfrac{1}{r_{n-2}}, c_n=\dfrac{1}{r_n}$ as two solutions of variable $x$, then we get the equation
$2(\dfrac{1}{2^2}+\dfrac{1}{1}+c_{n-1}^2+x^2)=(-\dfrac{1}{2}+\dfrac{1}{1}+c_{n-1}+{x})^2$
$\implies x^2-(2c_{n-1}+1)x+(c_{n-1}^2-c_{n-1}+\dfrac{9}{4})=0$
Via Vieta’s Formula we know that
$c_{n-2}+c_n=2c_{n-1}+1 \implies c_n-c_{n-1}=c_{n-1}-c_{n-2}+1$
Let $d_n\triangleq c_n-c_{n-1} \implies d_n=d_{n-1}+1$
$r_1=1, r_2=\dfrac{2}{3} \implies c_1=1, c_2=\dfrac{3}{2} \implies d_2=\dfrac{1}{2} \implies d_n=d_2+(n-2)=\dfrac{1}{2}+(n-2) \implies c_n-c_{n-1}=n-\dfrac{3}{2}$
$\implies c_n=d_n+c_{n-1}=d_n+d_{n-1}+c_{n-2}=…=\displaystyle \sum_{i=2}^{n}{d_i}+c_1=\displaystyle \sum_{i=2}^{n}{(i-\dfrac{3}{2})}+1$
$=\displaystyle \sum_{i=2}^{n}{i}-(n-1)\dfrac{3}{2}+1=\dfrac{n(n+1)}{2}-1-\dfrac{3n-3}{2}+1=\dfrac{n^2-2n+3}{2}$
$\implies r_n=\dfrac{1}{c_n}=\dfrac{2}{n^2-2n+3}$
The total length of segments is
$\displaystyle 2\sum_{i=1}^{\infty}{r_i}-r_1= 2\sum_{i=1}^{\infty}{\dfrac{2}{i^2-2i+3}}-1=4\sum_{i=1}^{\infty}{\dfrac{1}{(i-1)^2+2}}-1=4\sum_{i=0}^{\infty}{\dfrac{1}{i^2+2}}-1$
Now the task is to calculate the sum of infinite series.
$\dfrac{sin(\pi x)}{\pi x}=\displaystyle \prod_{n=1}^{\infty}{(1-\dfrac{x^2}{n^2})} \implies [ln\dfrac{sin(\pi x)}{\pi x}]’=\sum_{n=1}^{\infty}{ln[(1-\dfrac{x^2}{n^2})]’}$
$\implies \dfrac{\pi x}{sin(\pi x)}\cdot\dfrac{\pi cos(\pi x)\cdot \pi x -\pi sin(\pi x)} {(\pi x)^2}=\dfrac{\pi cos(\pi x)}{sin(\pi x)}-\dfrac{1}{x}=\displaystyle \sum_{n=1}^{\infty}{\dfrac{n^2}{n^2-x^2}\cdot(\dfrac{-2x}{n^2})}=-\sum_{n=1}^{\infty}{\dfrac{2x}{n^2-x^2}}$
$\implies \displaystyle \sum_{n=1}^{\infty}{\dfrac{1}{n^2-x^2}}=\dfrac{1}{2x^2}-\dfrac{\pi cot(\pi x)}{2x}$
Let $x=-ik \implies \displaystyle \sum_{n=1}^{\infty}{\dfrac{1}{n^2+k^2}}=-\dfrac{1}{2k^2}+\dfrac{\pi cot(-i k \pi)}{2ik}$
Use equity $cot (x) = i cot (ix) \implies \displaystyle \sum_{n=1}^{\infty}{\dfrac{1}{n^2+k^2}}=-\dfrac{1}{2k^2}+\dfrac{\pi cot(k\pi )}{2k}$
So the total length of segments is:
$4\displaystyle \sum_{i=0}^{\infty}{\dfrac{1}{i^2+(\sqrt{2})^2}}-1=4(\dfrac{1}{2}-\dfrac{1}{2*(\sqrt{2})^2}+\dfrac{\pi cot(\sqrt{2}\pi)}{2\sqrt{2}})-1=\sqrt{2}\pi cot(\sqrt{2} \pi)$
$=\sqrt{2}\pi\dfrac{exp(\sqrt{2}\pi)+exp(-\sqrt{2}\pi)}{exp(\sqrt{2}\pi)-exp(-\sqrt{2}\pi)}\approx 4.4441$
Solve 2:
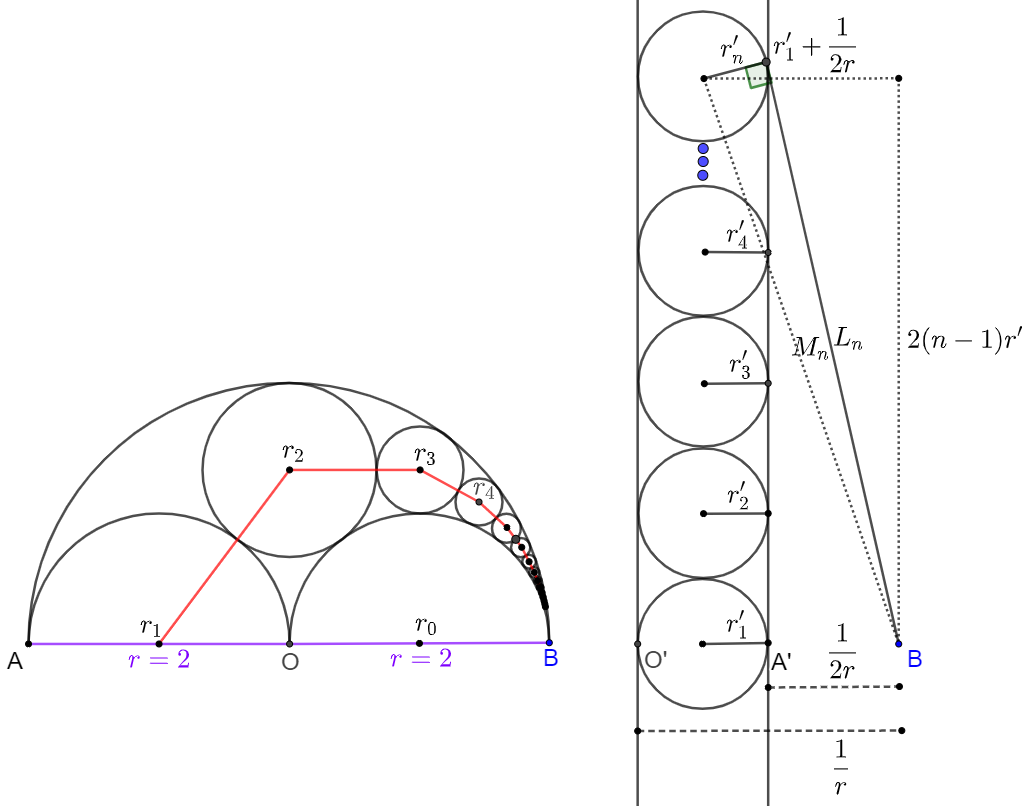
Reflect the figure via unit circle centered at $B$. Circles centered at $O, r_0$ will be parallel lines $O’, A’$ in distance of $\dfrac{1}{r}, \dfrac{1}{2r}$ to $B$.
Circles $r_1, r_2, r_3, r_4, …, r_n$ are tangent to circles centered at $r_0, O$ and the reflected circles centered at $r_1’, r_2’, r_3’, r_4’,…,r_n’$ are kept tangent to lines $O’, A’$.
$r’=r_1’=r_2’=r_3’=r_4’=…=r_n’=\dfrac{\dfrac{1}{r}-\dfrac{1}{2r}}{2}=\dfrac{1}{4r}$
The relationship of $r_n$ is got by the length of tangent line from $B$, the center of inversion, to the circle $r_n$:
$L_n^2=\dfrac{r’}{r_n}$
where $L_n^2=M_n^2-r’^2$
$M_n^2=(r’+\dfrac{1}{2r})^2+[2(n-1)r’]^2$
$\implies r_n=\dfrac{r}{(n-1)^2+2}=\dfrac{r}{n^2-2n+3}$
The rest part to calculate the series of segments is the same as solution 1.
Note for reading:
Example:
-
Add a line with two points $F$ and $G$
-
Add a circle with definition as $Reflect(Line(F, G), C)$
- Sacred Mathematics : Japanese Temple Geometry
- 算额 Wiki
- 绘马 Wiki
- Pappus chain Wiki
- Arbelos Wiki
- Inversive geometry Wiki
- Reflections on the Arbelos
- Circle Inversions and Applications to Euclidean Geometry
- Euclidean plane and its relatives
- Equity proof 1
- Equity proof 2
09/19/2021
$MN=1$, randomly pick points $P,Q$ on $MN$, what is the possibility that $MP, PQ, QN$ can be three sides of a triangle?
Solve:
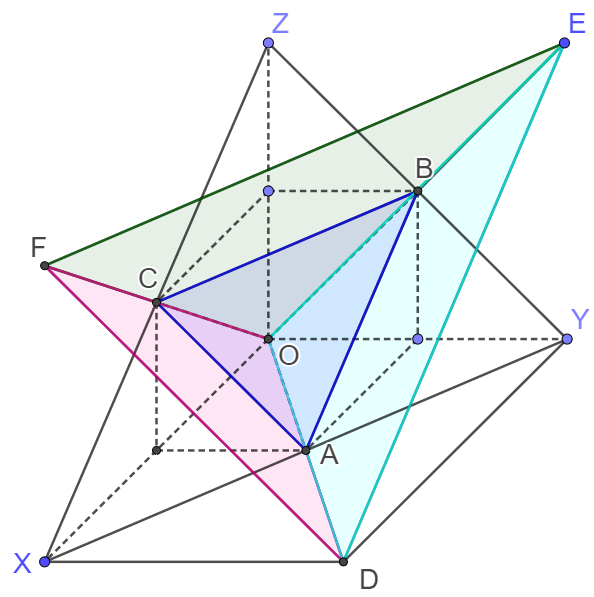
Let the length of three sides are $MP=x, PQ=y, QN=z$, the equation $x+y+z=1$ and $x>0, y>0, z>0$ forms the area of $\triangle{XYZ}$ with $OX=OY=OZ=1$
The equation $y=x+z$ and $x>0,y>0,z>0$ forms the part of plane $ODE$ and it intersects with $\triangle{XYZ}$ on the line $AB$.
The equation $z=x+y$ and $x>0,y>0,z>0$ forms the part of plane $OEF$ and it intersects with $\triangle{XYZ}$ on the line $BC$.
The equation $x=y+z$ and $x>0, y>0, z>0$ forms the part of plane $ODF$ and it intersects with $\triangle{XYZ}$ on the line $CA$.
$A,B,C$ are midpoints of $XY,YZ,ZX$.
The restriction $x<y+z, y<z+x, z<x+y, x>0,y>0,z>0$ forms the triangular pyramid $ODEF$ and it intersects with $\triangle{XYZ}$ on the $\triangle{ABC}$.
so $p_=\dfrac{S_{\triangle{ABC}}}{S_{\triangle{XYZ}}}=\bbox[1px, border: 1px solid black]{\dfrac{1}{4}}$
09/22/2021
Use only a ruler to get the perpendicular line from point $A$ on a circle with diameter $BC$.
Solve:
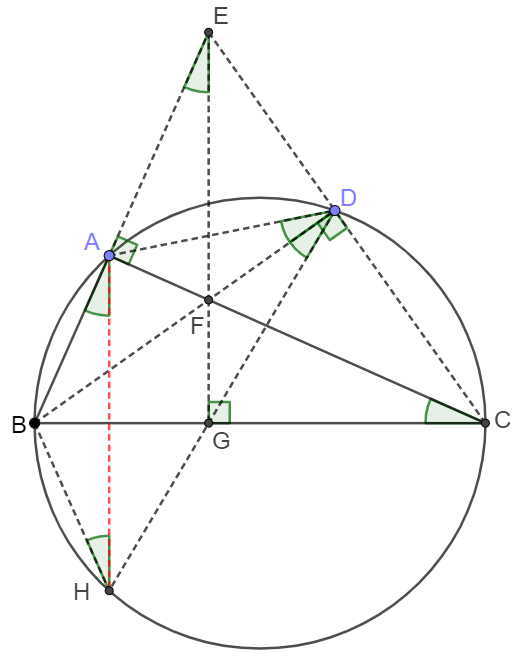
Pick $D$ as be any other point on the same side of $BC$ as $A$ on the circle.
Let $E$ be the intersect of extended $BA$ and $CD$, $F$ be the intersect of $AC$ and $BD$, $G$ be the intersect of $BC$ and extended $EF$.
Let $H$ be the intersect of the circle and extended $DG$. Connect $AH, BH$.
In $\triangle{EBC}$, $BD\perp EC, AC \perp BE$, $\implies F$ is the orthocenter of $\triangle{EBC} \implies EG \perp BC$
$\implies \text {C, D, F, G are cyclic} \implies \angle{ACB}=\angle{BDH}=\angle{BAH}$
$\implies \angle{CBA}+\angle{BAH}=\angle{CBA}+\angle{ACB}=90^{\circ}\implies AH \perp BC\blacksquare$
Some people asked for Chinese version on Weibo. Here is it:
在圆上任取点$D$与$A$在直径$BC$同侧。令$E$为$BA$延长线与$CD$延长线交点,$F$为$AC$与$BD$交点,$G$为$BC$与$EF$延长线交点。
令$H$为$DG$延长线与圆交点。连接$AH$,$BH$。
在 $\triangle{EBC}$内, $BD\perp EC, AC \perp BE$, $\implies F$ 为 $\triangle{EBC}垂心 \implies EG \perp BC$
$\implies \text {C, D, F, G 四点共圆} \implies \angle{ACB}=\angle{BDH}=\angle{BAH}$
$\implies \angle{CBA}+\angle{BAH}=\angle{CBA}+\angle{ACB}=90^{\circ}\implies AH \perp BC\blacksquare$