08/04/2021

$D$​ is a point on $BC$​ in $\triangle{ABC}, $\angle{DAC}=60^{\circ}, \angle{DCA}=40^{\circ}, BD=AC$​, Solve $\angle{B}$​​.

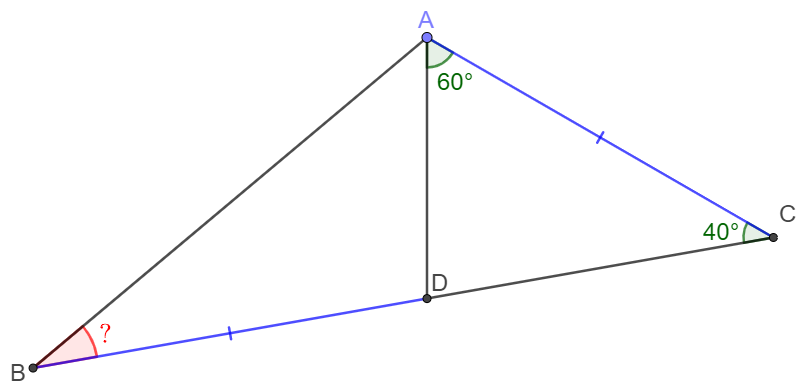
Solve:

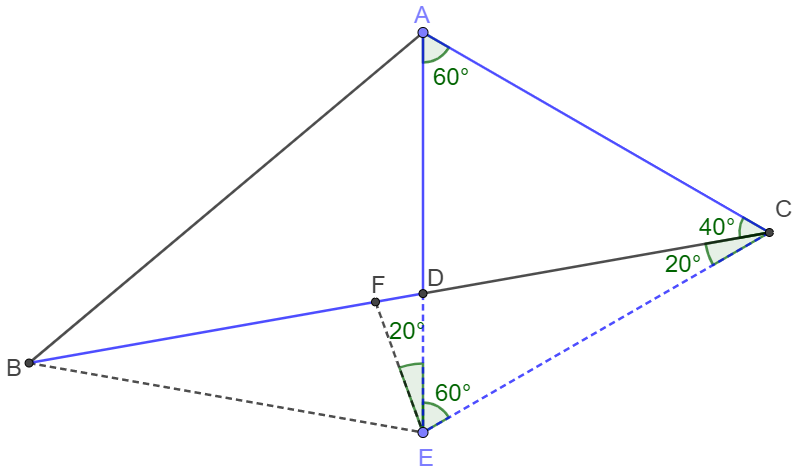
Extend $AD$​ to $E$​ so that $AE=AC$​, connect $CE$​. Easy to know $\triangle{ACE}$​ is equilateral, so

$\angle{AEC}=60^{\circ}, AE=AC=CE. \angle{DCE}=20^{\circ} \implies \angle{BDE}=80^{\circ}$​

Make $F$​ on $BD$​ so that $\angle{FED}=20^{\circ}$​, easy to see that $EF=DE, \angle{EFC}=80^{\circ}=\angle{FEC} \implies CE=CF=BD \implies BF=CD$

$\angle{BFE}=\angle{EDC}=100^{\circ} \implies \triangle{BEF}\cong\triangle{CED}\implies BE=CE=AE, \angle{EBF}=\angle{ECD}=20^{\circ},\angle{BEF}=\angle{CED}=60^{\circ}$

$\implies \angle{BEA}=80^{\circ}\implies \angle{EBA}=50^{\circ} \implies \angle{ABF}=50^{\circ}-20^{\circ}=\bbox[1px, border: 1px solid black]{30^{\circ}}$​​​