07/03/2021
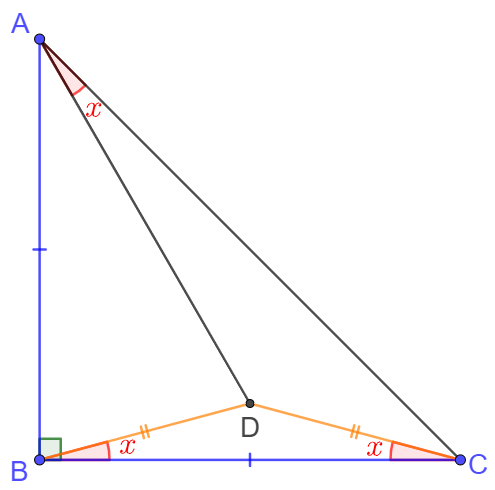
Solve angle $x$.
Solve 1：
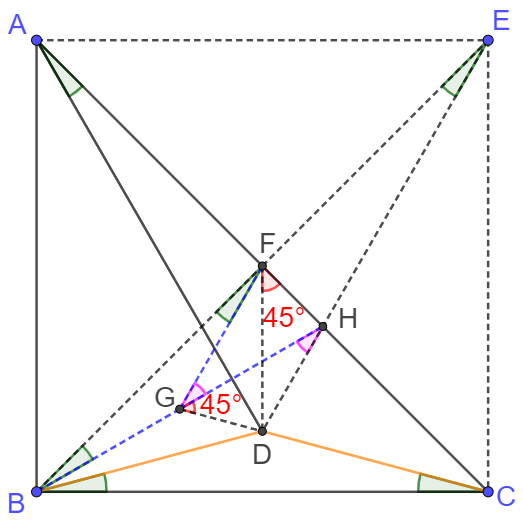
Make $ABCE$ a square. Connect $BE$. $BE$ and $AC$ intersect at $F$. Connect $DE$. $DE$ and $AC$ intersect at $H$.
Easy to see by symmetry that $\angle{ADB}=\angle{EDC}, \angle{DAC}=\angle{DEB}$, and $\triangle{BCF}$ is also an isosceles right triangle, $BF=EF=FC$
Make $G$ inside it so that $\angle{GBF}=\angle{GFB}=\angle{BCG}$, then we know $\angle{GCB}=\angle{DCB} \implies$ $C,D,G$ is collinear.
Connect $GH$, since $\angle{DAC}=\angle{DEB}=\angle{GBF}$, we know that $B,G,H$ is collinear.
Connect $DF$. Easy to see from symmetry that $\angle{DFC}=45^{\circ}$, $\angle{HGC}=\angle{GBC}+\angle{GCB}=\angle{GBC}+\angle{GBF}=45^{\circ}$
$\implies G,D,H,F$ are cyclic $\implies \angle{GFD}=\angle{GHD}$
$\angle{BFG}=\angle{BED} \implies FG \parallel DE \implies \angle{FGH}=\angle{GHD} \implies \angle{GFD}=\angle{FGH}=\angle{GBF}+\angle{BFG}$
$\implies \angle{BFD}=45^{\circ}=\angle{BFG}+\angle{GBF}+\angle{BFG}=3\cdot\angle{BFG} \implies \angle{BFG}=15^{\circ}$
$\implies \angle{CAD}=\angle{BFG}=\angle{BCD}=\bbox[1px, border: 1px solid black]{15^{\circ}}$
Solve 2:
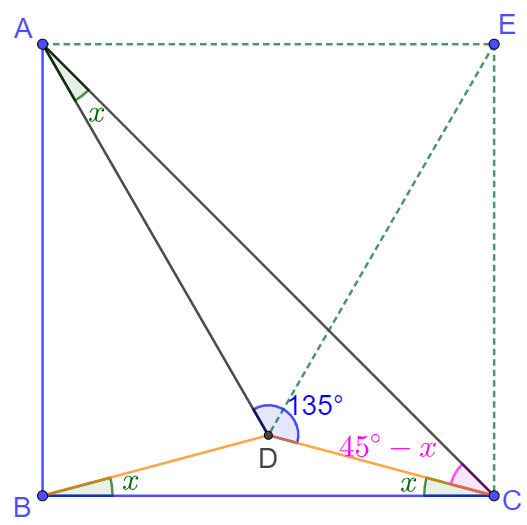
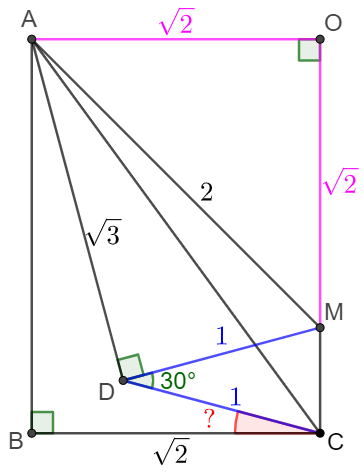
$\angle{DAC}=x, \angle{ACD}=45^{\circ}-x \implies \angle{ADC}=135^{\circ}$
Let $E$ be the circumcenter of $\triangle{ACD}$, easy to know that
$EA=ED=EC, \angle{AEC}=(180^{\circ}-135^{\circ}) * 2=90^{\circ}$
So $ABCE$ is a square
$AB=CE, BD=CD, \angle{ABD}=\angle{ECD} \implies \triangle{ABD} \cong \triangle{ECD}$
$\implies EA=ED=EC=AB=CD \implies \angle{AED}=60^{\circ}$
$\implies \angle{DEC}=90^{\circ}-60^{\circ}=30^{\circ}\implies \angle{DAC}=\dfrac{1}{2}\angle{DEC}=\bbox[1px, border: 1px solid black]{15^{\circ}}$
Solve 3:
$\angle{DAC}=x, \angle{ACD}=45^{\circ}-x \implies \angle{ADC}=135^{\circ}$
Let $AB=AC=a, BD=CD=b$
In $\triangle{ACD}$: $\dfrac{AC}{sin135^{\circ}}=\dfrac{CD}{sinx} \implies 2a*sinx=b$
In $\triangle{BCD}$: $\dfrac{BC}{sin(2x)}=\dfrac{BD}{sinx}\implies asinx=bsin(2x)=2asinxsin(2x)$
$\implies sin(2x)=\dfrac{1}{2}\implies 2x=30^{\circ} \implies x=\bbox[1px, border: 1px solid black]{15^{\circ}}$
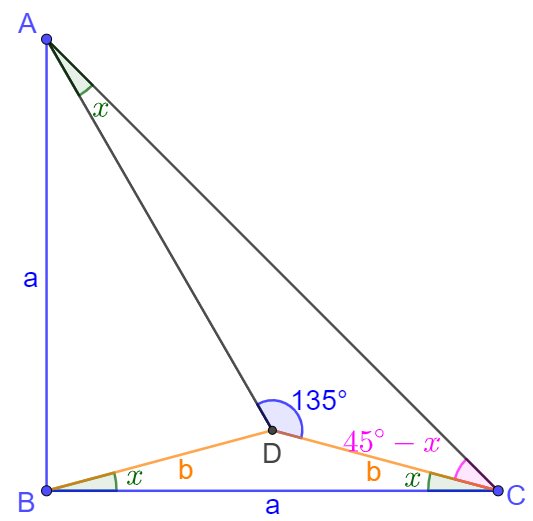
Solve4:
From Trigonometric Form of Ceva’s Theorem
$\dfrac{sin(45^{\circ}-x)}{sinx}\dfrac{sin(45^{\circ}-x)}{sinx}\dfrac{sinx}{sin(90^{\circ}-x)}=1$
$\implies sin^2(45^{\circ}-x)=sinx*cosx$
$\implies (sin45^{\circ}cosx-cos45^{\circ}sinx)^2=sinx*cosx$
$\implies 4sinx*cosx=1 \implies sin(2x)=\dfrac{1}{2} \implies 2x=30^{\circ}\implies x=\bbox[1px, border: 1px solid black]{15^{\circ}}$
07/04/2021
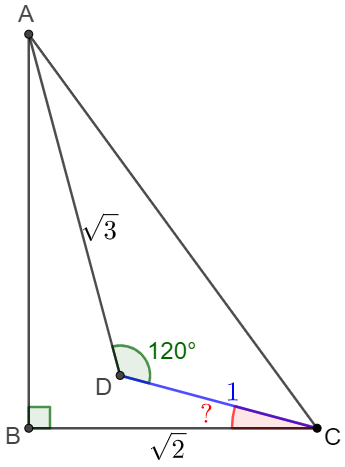
Solve angle $x$.
Solve:
Draw $MD \perp AD$ and $MD=CD=1$, easy to see that $AM=2, \angle{CDM}=30^{\circ} \implies \angle{MCD}=75^{\circ}$
Draw $AO\perp MO$ and $AO=MO$, easy to see that $AO=MO=\sqrt{2}$
$cos(\angle{ADC})=cos120^{\circ}=\dfrac{AD^2+CD^2-AC^2}{2CDAD}=\dfrac{4-AC^2}{2\sqrt{3}}=-\dfrac{1}{2} \implies AC^2=4+\sqrt{3}$
$\implies CO^2=AC^2-AO^2=4+\sqrt{3}-2=2+\sqrt{3}$
$cos(\angle{CDM})=cos30^{\circ}=\dfrac{CD^2+MD^2-CM^2}{2CDMD}=\dfrac{2-CM^2}{2}=\dfrac{\sqrt{3}}{2}\implies CM^2=2-\sqrt{3}$
$\implies CM^2=\dfrac{4-2\sqrt{3}}{2}=\dfrac{(\sqrt{3}-1)^2}{2}\implies CM=\dfrac{\sqrt{3}-1}{\sqrt{2}}$
$\implies (CM+MO)^2=(\dfrac{\sqrt{3}-1}{\sqrt{2}}+\sqrt{2})^2=(\dfrac{\sqrt{3}-1+2}{\sqrt{2}})^2=\dfrac{4+2\sqrt{3}}{2}=2+\sqrt{3}=CO^2$
$\implies CM+MO=CO \implies C,M,O$ are collinear $\implies \triangle{ABC}\cong \triangle{AOC}$
$\implies OC\perp BC \implies \angle{BCD}=90^{\circ}-\angle{DCM}=\bbox[1px, border: 1px solid black]{15^{\circ}}$
07/14/2021
$\triangle{ABC}$ is equilateral triangle. Point $D$ is outside the triangle and $AD=AB, \angle{DAB}=36^{\circ}$. Point $E$ is on $BD$ and $AE\perp BD$. $F$ is a point on $AE$ so that $\angle{BFC}=72^{\circ}$ and $AF$ is as short as possible. Prove $DF=FB=DB$
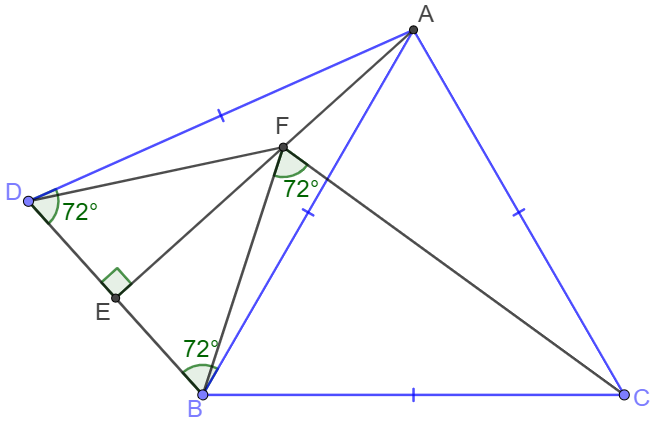
Prove 1:
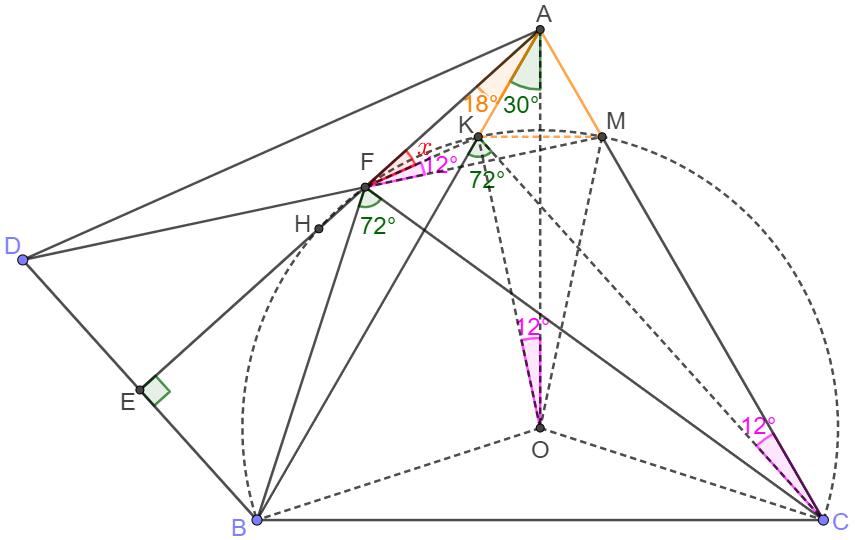
Suppose the center of circumcircle of $\triangle{BFC}$ is $O$; the circle and $AB, AC$ intersect respectively at $K,M$. The circle and AE intersect at $F, H$ where $F$ is closer to $A$. Connect $AO$. Easy to see that $\triangle{AKM}$ is equilateral, $\angle{KAO}=30^{\circ}, \angle{FAK}=18^{\circ}$
$\angle{BKC}=\angle{BFC}=72^{\circ} \implies \angle{ACK}=\angle{BKC}-\angle{KAC}=72^{\circ}-60^{\circ}=12^{\circ}=\angle{KFM}$
$\implies \angle{KOM}=2\angle{KCM}=24^{\circ}=2\angle{KOA}\implies \angle{KOA}=12^{\circ}$
Suppose $KA=KM=b, KF=c, \angle{KFA}=x$, then
$\angle{KMF}=180^{\circ}-\angle{FAK}-\angle{KAM}-\angle{KFA}-\angle{KFM}-\angle{KMA}=180^{\circ}-18^{\circ}-60^{\circ}-x-12^{\circ}-60^{\circ}=30^{\circ}-x$
In $\triangle{AFK}$: $\dfrac{AK}{sin(\angle{AFK})}=\dfrac{FK}{sin(\angle{FAK})}\implies \dfrac{b}{sinx}=\dfrac{c}{sin18^{\circ}}$
In $\triangle{FKM}$: $\dfrac{KM}{sin(\angle{KFM})}=\dfrac{FK}{sin(\angle{KMF})}\implies \dfrac{b}{sin12^{\circ}}=\dfrac{c}{sin(30^{\circ}-x)}$
$\implies sin12^{\circ} \cdot sin18^{\circ}=sinx \cdot sin(30^{\circ}-x) \implies \dfrac{1}{2}(cos6^{\circ}-cos30^{\circ})=\dfrac{1}{2}(cos(2x-30^{\circ})-cos30^{\circ})$
$\implies cos(2x-30^{\circ})=cos6^{\circ} \implies 2x-30^{\circ}=\pm 6^{\circ} \implies x=18^{\circ}$ or $x=12^{\circ}$
Since $F$ is closer to $A$ than $H$, $\angle{AFK} > \angle{AHK} \implies \angle{AFK}=x=18^{\circ}$
$\implies \angle{KMF}=30^{\circ}-x=12^{\circ}=\angle{FBK} \implies \angle{EFB}=\angle{FAK}+\angle{FBA}=30^{\circ}$
$\implies \angle{DFB}=2\angle{EFB}=60^{\circ}$, and since $DF=BF$, easy to see $\triangle{DFB}$ is equilateral, so $DF=FB=DB \blacksquare{}$
Prove 2:
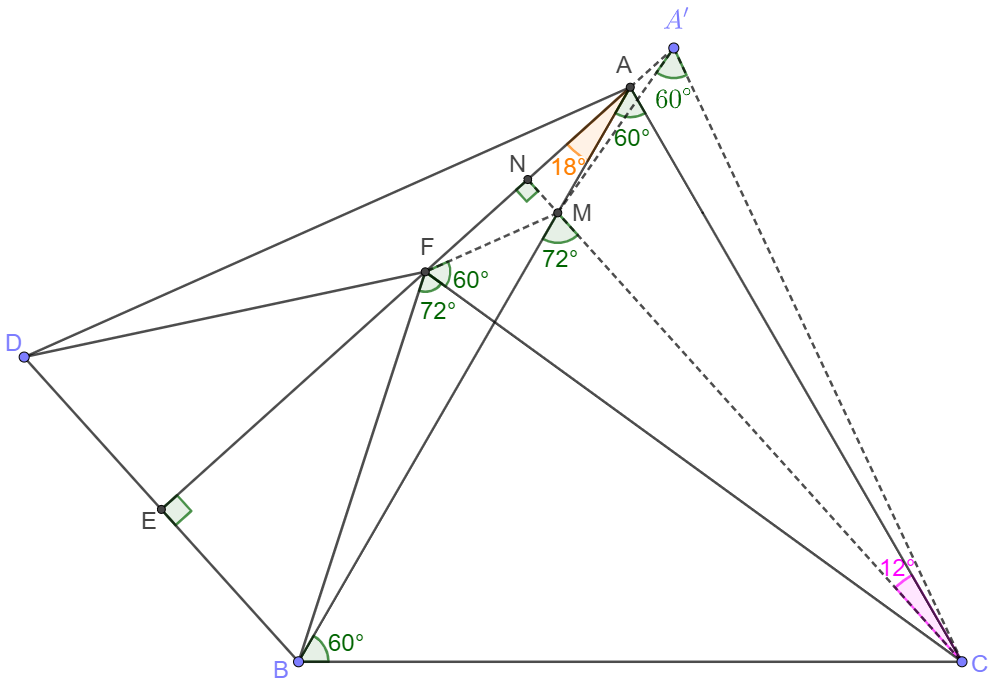
Make $CN \perp AF$ and $N$ on $AF$. $CN$ and $AB$ intersects at $M$.Connect FM.
$\angle{FAM}=18^{\circ} \implies \angle{NMA}=\angle{BMC}=72^{\circ}=\angle{BFC}$
$\implies B,F,M,C$ are cyclic, $\angle{MCA}=\angle{BMC}=\angle{BAC}=12^{\circ}, \angle{FBM}=\angle{FCM}$
$\implies \angle{MFC}=\angle{MBC}=60^{\circ}$
Suppose the reflection point of $F$ across $CN$ is $A’$.
(1) If $A’=A$, then $\angle{FBM}=\angle{FCM}=\angle{ACM}=12^{\circ} \implies \angle{EFB}=30^{\circ}\implies DB=DF=FB$
(2) If $A’ \neq A$, then connect $MA’$ and $CA’ \implies \triangle{CFM} \cong \triangle{CA’M}$
$\implies \angle{MA’C}=\angle{CFM}=60^{\circ}=\angle{MAC}\implies M,A,A’,C$ are cyclic
$\implies \angle{FBM}=\angle{FCM}=\angle{MCA’}=\angle{FAM}=18^{\circ}$
In (2) $\angle{FBM}=18^{\circ}$, in (1) $\angle{FBM}=12^{\circ}$, easy to see that $AF$ in (1) is shorter than in (2). Thus We know that $DB=DF=FB \blacksquare$
Note: Here we can also use trigonometric functions to prove:
$\angle{FCN}=180^{\circ}-\angle{CFM}-\angle{MFN}=30^{\circ}-\angle{MFN}$
$MN=AM \cdot sin18^{\circ} = MF \cdot sin(\angle{MFN})$
$\dfrac{CM}{sin{\angle{CFM}}}=\dfrac{CM}{sin{60^{\circ}}}=\dfrac{CM}{sin{\angle{MAC}}}=\dfrac{MF}{sin(30^{\circ}-\angle{MFN})}=\dfrac{AM}{sin{12^{\circ}}}$
$\implies sin(\angle{MFN}) \cdot sin(30^{\circ}-\angle{MFN})=sin12^{\circ} \cdot sin18^{\circ}$
The rest will be the same as proof 1.
07/25/2021
$\triangle{ABC}$ is equilateral. Points $E,F,G$ are inside it and form four triangles so that $S_{11}=S_{21}=S_{31}=S_4$. Find $\dfrac{AF}{FG}$.
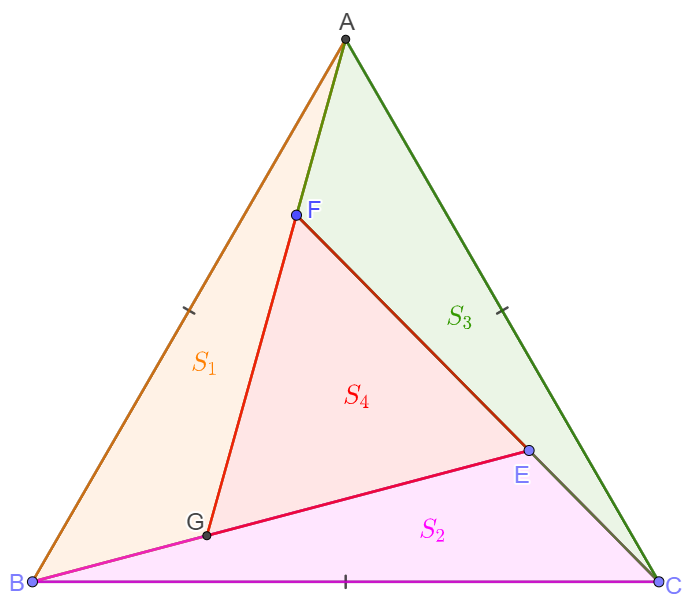
Solve: 1
Choose Barycentric coordinate, $A(1,0,0), B(0,1,0), C(0,0,1)$
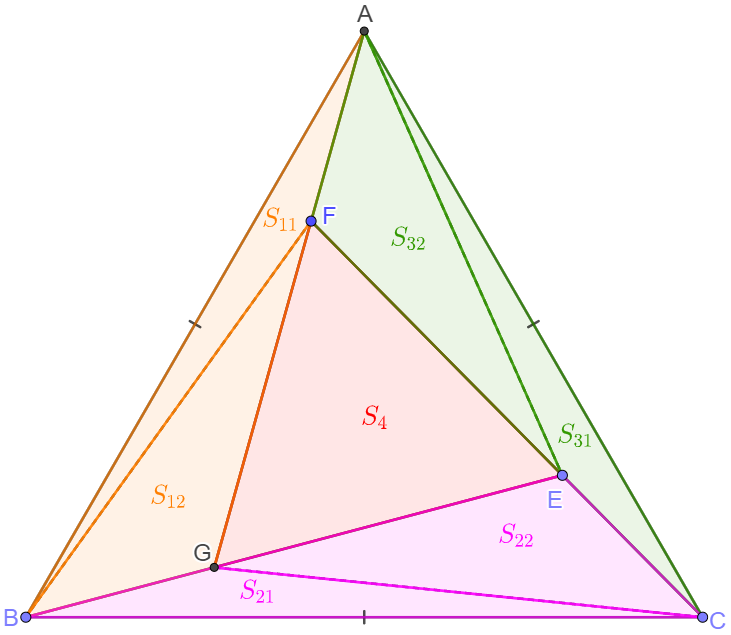
Let $S_{\triangle{BCG}}=S_{21}, S_{\triangle{ACE}}=S_{31}, S_{\triangle{ABF}}=S_{11}, S_{\triangle{ABC}}=S$, then
$E(\dfrac{1}{4}, \dfrac{S_{31}}{S}, \dfrac{3}{4}-\dfrac{S_{31}}{S}), F(\dfrac{3}{4}-\dfrac{S_{11}}{S}, \dfrac{1}{4}, \dfrac{S_{11}}{S}), G(\dfrac{S_{21}}{S}, \dfrac{3}{4}-\dfrac{S_{21}}{S}, \dfrac{1}{4})$ \(\begin{align*} CEF \text{ collinear } \implies \begin{vmatrix} \dfrac{3}{4}-\dfrac{S_{11}}{S} & \dfrac{1}{4} & 1 \\ \dfrac{1}{4} & \dfrac{S_{31}}{S} & 1 \\ 0 & 0 & 1 \end{vmatrix}=0 \implies 16S_{31}S_{11}-12SS_{31}+S^2=0 \implies S_{11}=\dfrac{3}{4}S-\dfrac{S^2}{16S_{31}}\\ BGE \text { collinear } \implies \begin{vmatrix} \dfrac{1}{4} & \dfrac{S_{31}}{S} & 1 \\ \dfrac{S_{21}}{S} & \dfrac{3}{4}-\dfrac{S_{21}}{S} & 1 \\ 0 & 0 & 1 \end{vmatrix}=0 \implies 16S_{21}S_{31}-12SS_{21}+S^2=0 \implies S_{21}=\dfrac{3}{4}S-\dfrac{S^2}{16S_{11}}\\ AFG \text{ collinear } \implies \begin{vmatrix} \dfrac{3}{4}-\dfrac{S_{11}}{S} & \dfrac{1}{4} & 1 \\ \dfrac{S_{21}}{S} & \dfrac{3}{4}-\dfrac{S_{21}}{S} & 1 \\ 1 & 0 & 1 \end{vmatrix}=0 \implies 16S_{11}S_{21}-12SS_{11}+S^2=0 \implies S_{31}=\dfrac{3}{4}S-\dfrac{S^2}{16S_{21}}\\ \end{align*}\) $\implies S_{11}=\dfrac{3}{4}S-\dfrac{S^2}{16(\dfrac{3}{4}S-\dfrac{S^2}{16S_{21}})}=\dfrac{3}{4}S-\dfrac{S}{12-\dfrac{S}{S_{21}}}=\dfrac{3}{4}S-\dfrac{S}{12-\dfrac{S}{\dfrac{3}{4}S-\dfrac{S^2}{16S_{11}}}}=\dfrac{3}{4}S-\dfrac{(12S_{11}-S)S}{128S_{11}-12S}$
$\implies 16S_{11}^2-12S_{11}S+S^2=0\implies S_{11}=\dfrac{3-\sqrt{5}}{8}S$ (remove the situation $S_{11}=\dfrac{3+\sqrt{5}}{8}S$)
$\implies S_{21}=\dfrac{3}{4}S-\dfrac{S^2}{16S_{11}}=\dfrac{3}{4}S-\dfrac{S^2}{16\dfrac{3-\sqrt{5}}{8}S}=\dfrac{3-\sqrt{5}}{8}S \implies S_{31}=\dfrac{3-\sqrt{5}}{8}S$
$\implies S_{21}=S_{31}=S_{11}$ (this step is to prove the symmetric conclusion that people take for granted)
$S_1=\dfrac{1}{4}S=S_{11}+S_{\triangle{BFG}}=\dfrac{3-\sqrt{5}}{8}S+S_{\triangle{BFG}}\implies S_{\triangle{BFG}}=\dfrac{\sqrt{5}-1}{8}S$
$\implies \dfrac{AF}{FG}=\dfrac{S_{11}}{S_{\triangle{BFG}}}=\dfrac{3-\sqrt{5}}{\sqrt{5}-1}=\bbox[1px, border: 1px solid black]{\dfrac{\sqrt{5}-1}{2}}$
Solve 2:
Let $\dfrac{S_{\triangle{BFG}}}{S_{\triangle{EFG}}}=\dfrac{S_{12}}{S_4}=x=\dfrac{BG}{GE}=\dfrac{S_{11}}{S_{32}}=\dfrac{S_{21}}{S_{22}}\implies S_{21}=\dfrac{x}{1+x}S_4, S_{22}=\dfrac{1}{1+x}S_4$
$\implies S_{11}=(1-x)S_4, S_{32}=\dfrac{1-x}{x}S_4 \implies S_{31}=S_4-S_{32}=S_4-\dfrac{1-x}{x}S_4=\dfrac{2x-1}{x}S_4$ $\dfrac{CE}{EF}=\dfrac{S_{31}}{S_{32}}=\dfrac{S_{22}}{S_4} \implies \dfrac{\dfrac{2x-1}{x}}{\dfrac{1-x}{x}}=\dfrac{\dfrac{1}{1+x}}{1}\implies x^2+x-1=0\implies x=\dfrac{\sqrt{5}-1}{2}$
$\implies \dfrac{AF}{FG}=\dfrac{S_{11}}{S_{12}}=\dfrac{1-x}{x}=x=\bbox[1px, border: 1px solid black]{\dfrac{\sqrt{5}-1}{2}}$
Note 1: this solution does not take $\triangle{ABC}$ as equilateral triangle, and seems the result to be more general to all triangles.
Note 2: Tran Quang Hung has posted on the CutTheKnotMath facebook page an elegant occurrence of the golden ratio in equilateral triangles