05/04/2021
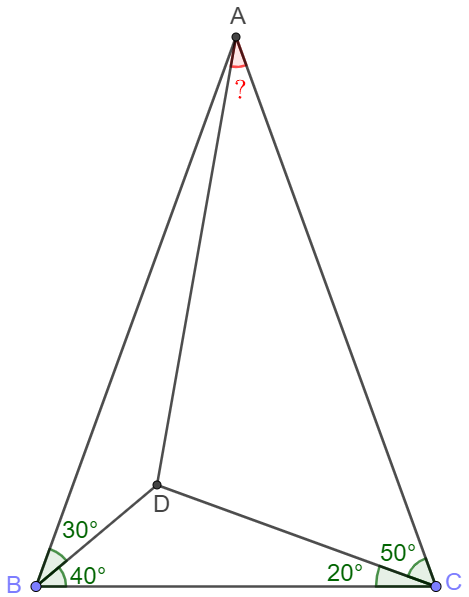
Solute:
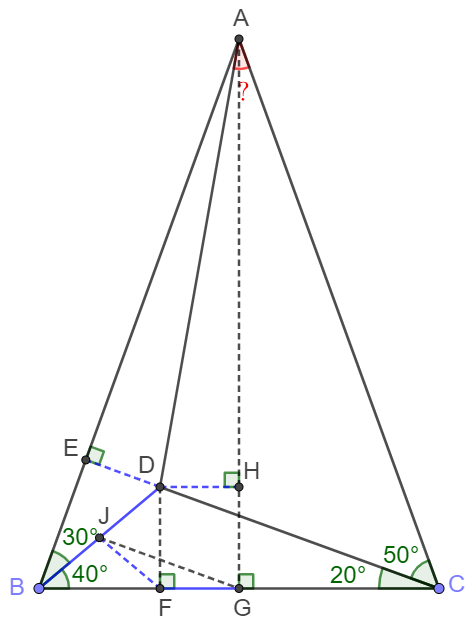
From $A$ and $D$ make line $AG$ perpendicular to $BC$ at $G$, $DF$ perpendicular to $BC$ at $F$.
Extend $CD$ till $AB$ at $E$. From $G$ make $JG \parallel CD$ and meet $BD$ at $J$ . Connect $FJ$.
$\angle{ABC}=\angle{ACB}=70^{\circ} \implies BG=CG$
and $JG \parallel CD \implies BJ=JD$
and $\angle{BFD=90^{\circ} \implies FJ=JD=BJ}$
Easy to see that $CE \perp AB \implies DE=JD=BJ=JF$
$\implies \angle{JFB}=\angle{DBC}=40^{\circ}$
$JG \parallel CD \implies \angle{JGB}=\angle{BCD}=20^{\circ}$
$\implies \angle{FJG}=20^{\circ} \implies JF=FG=DH=DE$
$\implies \triangle{ADE}=\triangle{ADH}$
$\implies \angle{ADE}=\dfrac{1}{2}\angle{BAG}=\dfrac{1}{4}\angle{BAC}=10^{\circ}$
$\implies \angle{DAC}=\bbox[1px, border: 1px solid black]{30^{\circ}}$
05/05/2021
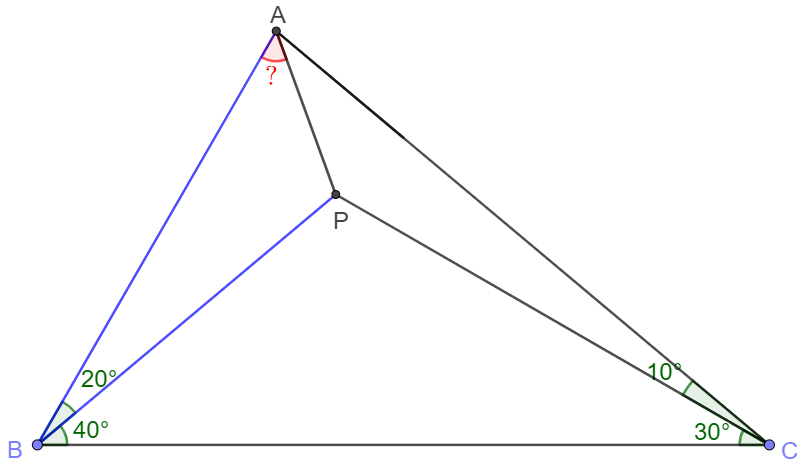
Solve:
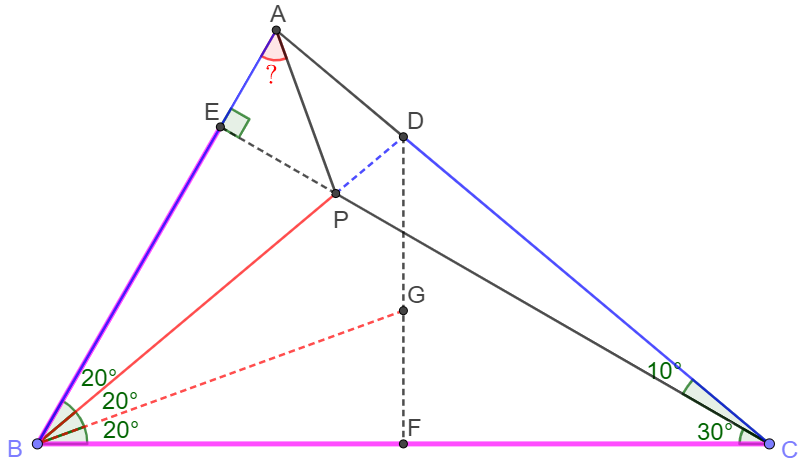
Extend $BP$ to meet $AC$ at $D$, extend $CP$ to meet $AB$ at $E$. Easy to see that $CE \perp AB$, $BD=CD$.
Make $DF \perp BC$ at $F$. Bisect $\angle{PBC}$ and meet $DF$ at $G$.
Easy to see that $\angle{GBF}=\angle{DBG}=\angle{ABP}=20^{\circ}$, $BF=CF \implies EF=BF$
$\angle{ABC}=60^{\circ} \implies BE=BF \implies \triangle{BEP} \cong \triangle{BFG} \implies BP=BG$
$\angle{ABD}=20^{\circ}, \angle{BAC}=80^{\circ} \implies \angle{ADB}=80^{\circ} \implies AB=BD$
$\implies \triangle{ABP} \cong \triangle{DBG} \implies \angle{BAP}=\angle{BPF}=90^{\circ}-\angle{DBF}=\bbox[1px, border: 1px solid black]{50^{\circ}}$
05/06/2021
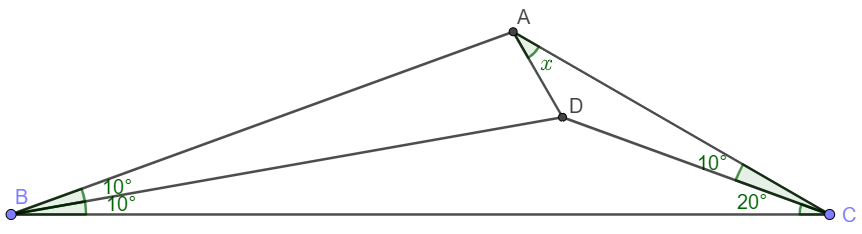
Solve 1:
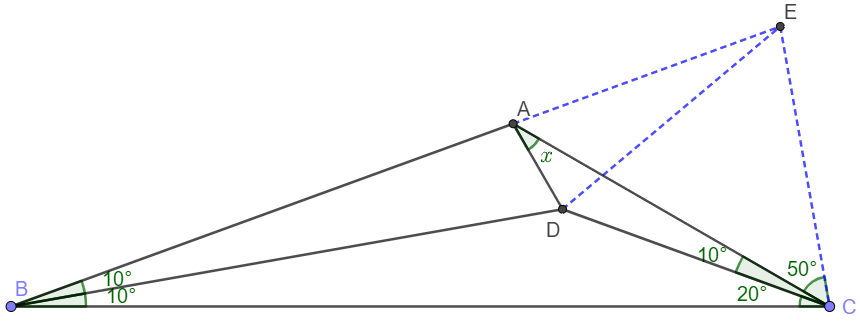
Extend $BA$ to $E$ so that $\angle{ECA}=50^{\circ}$. Easy to see that $\angle{EAC}=\angle{ECA}=50^{\circ} \implies EA=EC$
$\angle{ECB}=80^{\circ}=\angle{BEC} \implies BE=BC \implies \triangle{EBD} \cong \triangle{CBD} \implies DE=DC$
$\angle{DCE}=60^{\circ} \implies \triangle{DCE}$ is equilateral $\implies ED=EC=EA, \angle{DEC}=60^{\circ}$
$\implies \angle{AED}=20^{\circ} \implies \angle{EAD}=80^{\circ} \implies \angle{DAC}=80^{\circ}-50^{\circ}=\bbox[1px, border: 1px solid black]{30^{\circ}}$
Solve 2:
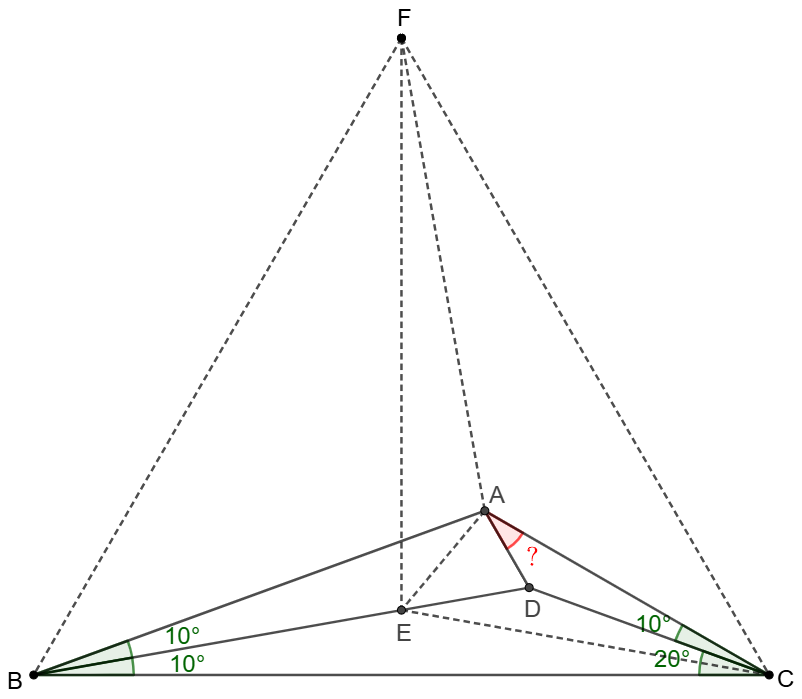 \(\begin{multline}
\shoveleft \text{Let }E \text{ be the isogonal conjugate of } D \text{ with respect to }\triangle{ABC}\\
\shoveleft \angle{ABD}=\angle{BCD}=10^{\circ}\implies \angle{ABE}=\angle{BCE}=10^{\circ}\\
\shoveleft \angle{ACD}=10^{\circ}\implies \angle{BCE}=10^{\circ}\implies BE=CE\\
\shoveleft \text{Let }F \text{ be the reflection of }B \text{ along }AC \implies \\
\shoveleft BC=FC, \angle{ACB}=\angle{ACF}=30^{\circ}, \angle{ABC}=\angle{AFC}=20^{\circ}\\
\shoveleft \implies \triangle{FBC} \text{ is equilateral }\implies \angle{EFB}=\angle{EFC}=30^{\circ}\\
\shoveleft \implies \angle{EFA}=10^{\circ}=\angle{EBA}\implies AEBF\text{ is cyclic}\\
\shoveleft \implies \angle{EAB}=\angle{EFB}=\angle{DAC}=\bbox[5px, border: 1px solid black]{30^{\circ}}
\end{multline}\)
\(\begin{multline}
\shoveleft \text{Let }E \text{ be the isogonal conjugate of } D \text{ with respect to }\triangle{ABC}\\
\shoveleft \angle{ABD}=\angle{BCD}=10^{\circ}\implies \angle{ABE}=\angle{BCE}=10^{\circ}\\
\shoveleft \angle{ACD}=10^{\circ}\implies \angle{BCE}=10^{\circ}\implies BE=CE\\
\shoveleft \text{Let }F \text{ be the reflection of }B \text{ along }AC \implies \\
\shoveleft BC=FC, \angle{ACB}=\angle{ACF}=30^{\circ}, \angle{ABC}=\angle{AFC}=20^{\circ}\\
\shoveleft \implies \triangle{FBC} \text{ is equilateral }\implies \angle{EFB}=\angle{EFC}=30^{\circ}\\
\shoveleft \implies \angle{EFA}=10^{\circ}=\angle{EBA}\implies AEBF\text{ is cyclic}\\
\shoveleft \implies \angle{EAB}=\angle{EFB}=\angle{DAC}=\bbox[5px, border: 1px solid black]{30^{\circ}}
\end{multline}\)
05/07/2021
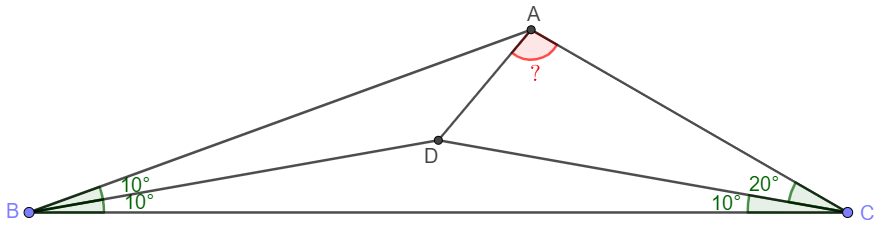
Solve:
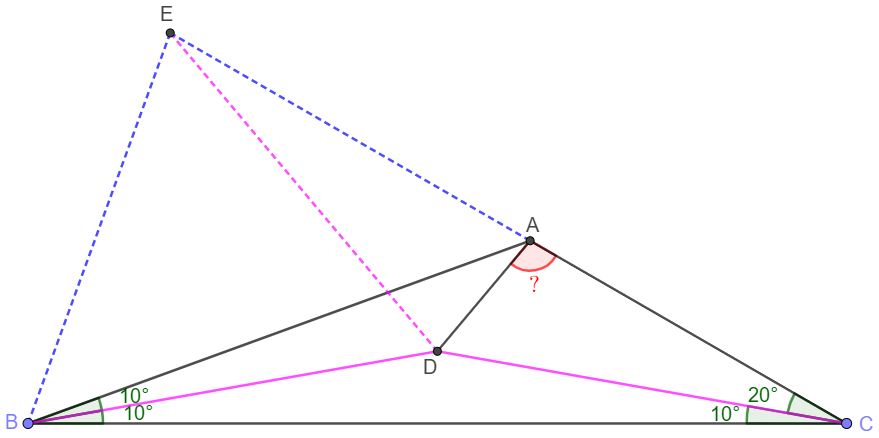
Extend $CA$ to $E$ so that$\angle{EBA}=50^{\circ}$. Easy to see that $\angle{EAB}=50^{\circ} \implies EA=EB, \angle{BEC}=80^{\circ}$
$DB=DC, \angle{BDC}=160^{\circ}=2 \cdot \angle{BEC} \implies D$ is the center of circumcircle of $\triangle{BEC}$
$\implies DE=DB=DC \implies \angle{DEC}=\angle{DCE}=20^{\circ} \implies \angle{EDB}=80^{\circ}-20^{\circ}=60^{\circ}$
$\implies \triangle{BDE}$ is equilateral $\implies DE=BE=EA \implies \angle{EAD}=80^{\circ} \implies \angle{DAC}=\bbox[1px, border: 1px solid black]{100^{\circ}}$
05/08/2021
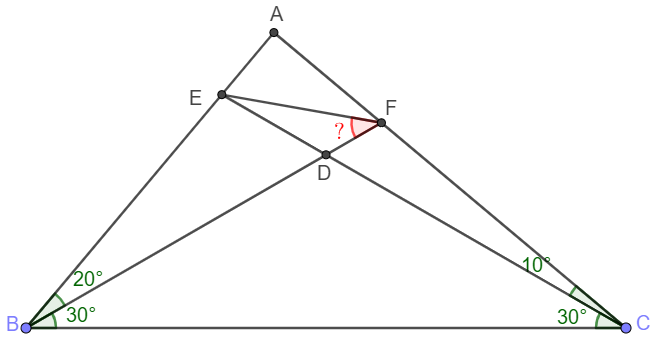
Solve:
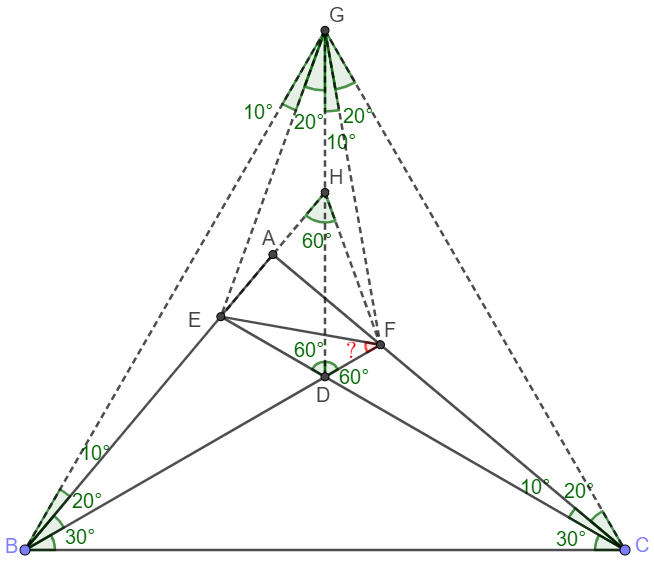
Make point $G$ so that $\angle{ABG}=10^{\circ}, \angle{ACG}=20^{\circ} \implies$ $\triangle{GBC}$ is equilateral and $D$ is its incenter.
$\implies \angle{EDG}=\angle{FDG}=60^{\circ}$
$\implies BE=GE \implies \angle{EBG}=\angle{EGB}=10^{\circ}, \angle{EGD}=\angle{EBD}=20^{\circ}$
$\implies CF=GF \implies \angle{FCG}=\angle{FGC}=20^{\circ}, \angle{DGF}=\angle{DCF}=10^{\circ}$
$\implies \angle{EGF}=30^{\circ}$
Connect $DG$, find point $H$ on $DG$ so that $\angle{EHF}=60^{\circ}$
Now we have the sum of opposite angles $\angle{EDF} + \angle{EHF}=180^{\circ}$
$\implies EHFD$ is cyclic
$\implies \angle{EFH}=\angle{EDH}=60^{\circ}, \angle{FEH}=\angle{FDH}=60^{\circ}$
$ \implies \triangle{EFH} $ is equilateral triangle $\implies EH=FH, \angle{EHF}=60^{\circ}$
$\angle{EGF}=30^{\circ} \implies$ $H$ is the circumcenter of $\triangle{GEF}$
$\implies GH=EH=FH \implies \angle{EFD}=\angle{EHD}=\bbox[1px, border: 1px solid black]{40^{\circ}}$
05/09/2021
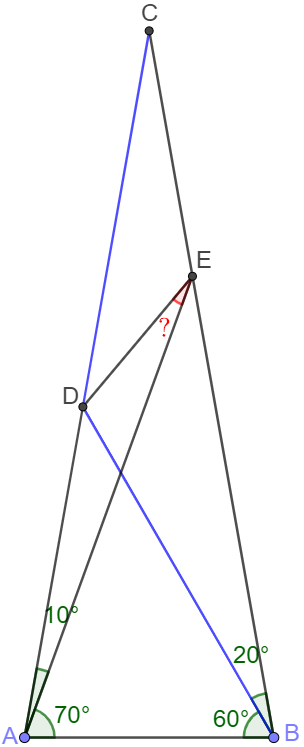
Solve 1:
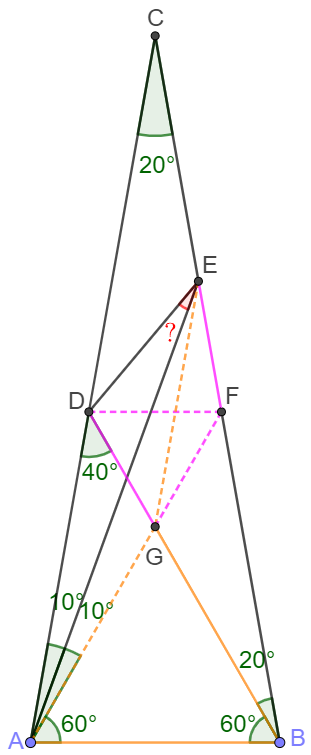
Let point $F$ on $BC$ so that $\angle{FAB}=60^{\circ}$. $AF$ and $BD$ intersect at $G$. Connect $EG$.
Easy to know that $\triangle{ABG}, \triangle{DFG}$ are equilateral triangles.
And easy to see that $CD=CF=BD=AF$
$\angle{AGB}=60^{\circ}, \angle{AEB}=30^{\circ}, AG=GB \implies G$ is the circumcenter of $\triangle{ABE}$
$\implies AG=GB=GE \implies \angle{GEB}=\angle{EBG}=20^{\circ}=\angle{ACB}$
$\implies EG \parallel AC \implies \dfrac{EF}{CF}=\dfrac{FG}{AF} \implies EF=FG \implies EF=DF$
$\implies \angle{DEF}=\angle{EDF}=\dfrac{180^{\circ}-\angle{EFD}}{2}=50^{\circ} \implies \angle{DEA}=50^{\circ}-30^{\circ}=\bbox[5px, border: 1px solid black]{20^{\circ}}$
Solve 2:
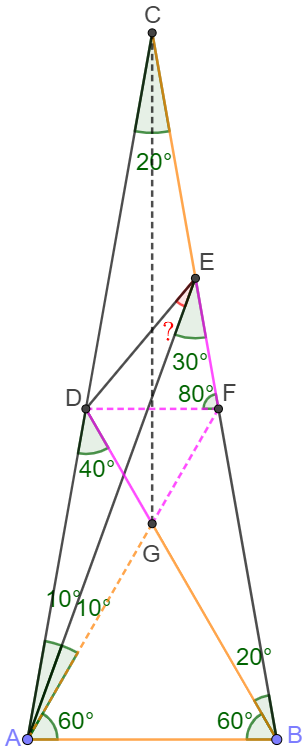
Let point $F$ on $BC$ so that $\angle{FAB}=60^{\circ}$. $AF$ and $BD$ intersect at $G$. Connect $CG$.
Easy to know that $\angle{AEB}=30^{\circ}$.
Easy to know that $\triangle{ABG}, \triangle{DFG}$ are equilateral triangles $\implies \angle{CFD}=80^{\circ}$.
Easy to know that $\triangle{DFG}$ is equilateral $\implies FG=DF$
Easy to know that $\angle{ACG}=\angle{BCG}=10^{\circ}$
$\implies \triangle{ACG} \cong \triangle{CAE}\implies CE=AG$
$\angle{FAC}=\angle{ACF}=20^{\circ} \implies AF=CF $
$\implies AF-AG=CF-CE \implies EF=FG=DF$
$\implies \angle{DEF}=\angle{EDF}=\dfrac{180^{\circ}-80^{\circ}}{2}=50^{\circ}$
$\implies \angle{DEA}=50^{\circ}-30^{\circ}=\bbox[5px, border: 1px solid black]{20^{\circ}}$
05/10/2021
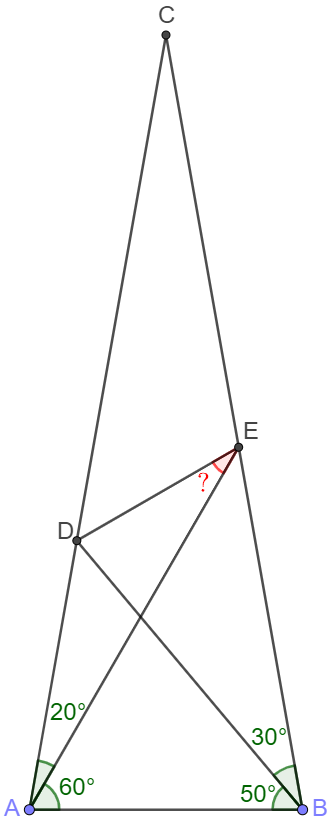
Solve 1:
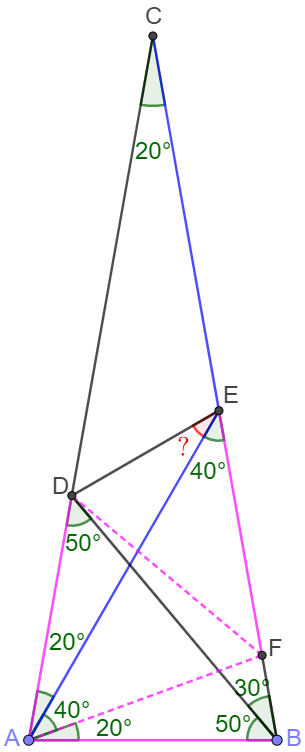
Make point $F$ on $BC$ so that $\angle{FAB}=20^{\circ} \implies AB=AF$
Since $\angle{ADB}=\angle{ABD}=50^{\circ} \implies AD=AB \implies AD=AF$
$\angle{DAF}=60^{\circ} \implies \triangle{ADF}$ is equilateral triangle $\implies DF=AF$
$\angle{EAF}=40^{\circ}=\angle{AEF} \implies AF=EF \implies DF=EF$
$\angle{DFE}=180^{\circ}-60^{\circ}-80^{\circ}=40^{\circ} \implies \angle{DEF}=70^{\circ}$
$\implies \angle{DEA}=\bbox[1px, border: 1px solid black]{30^{\circ}}$
Solve 2:
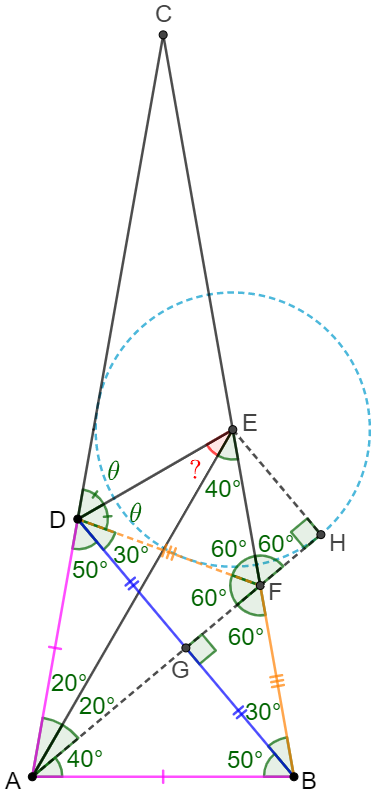
Make $F$ on $AC$ so that $EF \parallel AB$. Let $BF$ and $AE$ intersect at $G$.
Easy to see that $\triangle{ABG}$ and $EFG$ are equilateral so $AG=AB, EF=FG, \angle{FEG}=60^{\circ}$.
$\angle{ADB}=50^{\circ}=\angle{ABD} \implies AD=AB \implies AD=AG \implies \angle{AGD}=80^{\circ}$
$\implies \angle{DGF}=180^{\circ}-\angle{DGA}-\angle{FGE}=180^{\circ}-80^{\circ}-60^{\circ}=40^{\circ}=\angle{DFG}$
$\implies DF=DG$ and we already know $EF=FG \implies \triangle{DEF} \cong \triangle{DEG} $
$\implies \angle{DEF}=\angle{DEG}=\dfrac{\angle{FEG}}{2}=\dfrac{60^{\circ}}{2}=\bbox[1px, border: 1px solid black]{30^{\circ}}$
Solve 3:
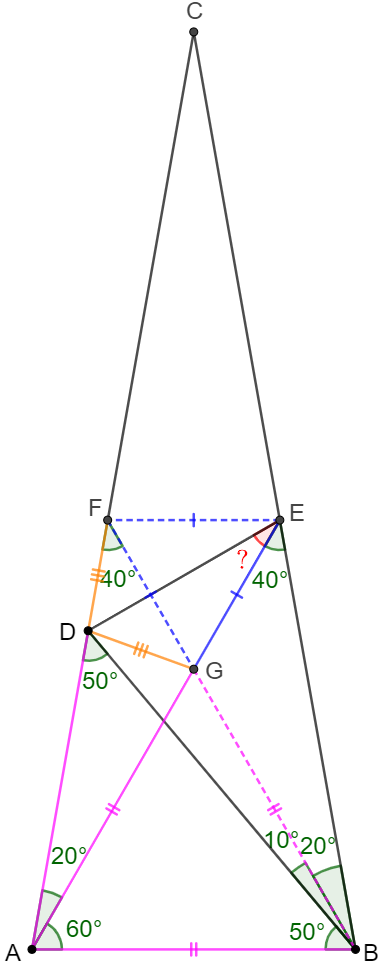
Make $F$ on $BC$ so that $\angle{FAE}=20^{\circ}$. Let $AF$ and $BD$ intersect at $G$. Extend $AF$ to $H$ so that $EH \perp AH$.
Easy to see that $\angle{GAB}=40^{\circ} \implies AG \perp BD \implies \angle{BFG}=90^{\circ}-\angle{FBG}=60^{\circ}$.
$\angle{ADB}=\angle{ABD}=50^{\circ} \implies AB=AD, \angle{DAG}=\angle{BAG}=40^{\circ} \implies \triangle{ADG} \cong \triangle{ABG} \implies DG=BG$
$\implies \triangle{DFG} \cong \triangle{BFG} \implies \angle{FDG}=\angle{FBG}=30^{\circ}, \angle{DFG}=\angle{BFG}=60^{\circ} $
$\implies \angle{DFE}=180^{\circ}-2*60^{\circ}=60^{\circ}=\angle{EFH}$
This mean $EF$ bisects $\angle{DFH}$ and $EA$ bisects $\angle{DAF}$, so $E$ is an excenter of $\triangle{ADF}$.
Then it means $DE$ bisects $\angle{CDF} \implies \angle{CDE}=\angle{EDF}=\dfrac{180^{\circ}-50^{\circ}-30^{\circ}}{2}=50^{\circ}$
$\implies \angle{DEA}=180^{\circ}-\angle{DAE}-\angle{ADB}-\angle{FDG}-\angle{EDF}=180^{\circ}-20^{\circ}-50^{\circ}-30^{\circ}-50^{\circ}=\bbox[1px, border: 1px solid black]{30^{\circ}}$
Solve 4:
Let $x=\angle{DEB}$. Easy to see that $AD=AB$, use the Law of Sines in $\triangle{ADE}$ and $\triangle{ABE}$:
$\dfrac{AE}{AD}=\dfrac{sin(160^{\circ}-x)}{sin x}$, $\dfrac{AE}{AB}=\dfrac{sin80^{\circ}}{sin40^{\circ}} \implies \dfrac{sin(160^{\circ}-x)}{sinx}=\dfrac{sin80^{\circ}}{sin40^{\circ}} $
$\implies sin(20^{\circ}+x)=2cos40^{\circ}sinx \implies sin20^{\circ}cosx+cos20^{\circ}sinx=2sinx \cdot cos(60^{\circ}-20^{\circ})$
$=2 sinx (cos60^{\circ} \cdot cos20^{\circ} + sin60^{\circ} \cdot sin20^{\circ}) = sinx \cdot cos20^{\circ}+2sinx \cdot sin60^{\circ}sin20^{\circ} $
$\implies sin20^{\circ}cosx=2sinx \cdot sin60^{\circ}sin20^{\circ} \implies cosx=2sinx \cdot sin60^{\circ}=\sqrt{3}sinx$
$\implies tan x = \dfrac{1}{\sqrt{3}} \implies x=\angle{AED}=\bbox[1px, border: 1px solid black]{30^{\circ}}$
Solve 5:
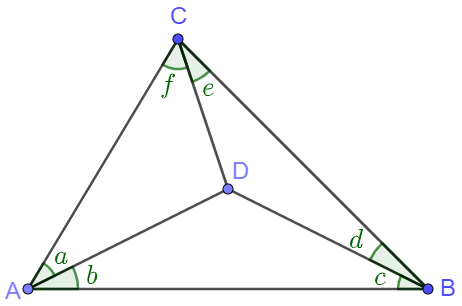
By angular form of Ceva’s Theorem we know that for a point $D$ inside $\triangle{ABC}$ as figure above there is
$\dfrac{sin(a)}{sin(b)} \dfrac{sin(c)}{sin(d)} \dfrac{sin(e)}{sin(f)} = 1$
$sin(e)=sin(180^{\circ}-(a+b+c+d+f))$
$=sin(a+b+c+d+f)=sin(a+b+c+d)cos(f)+cos(a+b+c+d)sin(f) $
$\implies sin(a)sin(c)sin(a+b+c+d+f)$
$=sin(a)sin(c)sin(a+b+c+d)cos(f)+sin(a)sin(c)cos(a+b+c+d)sin(f)$
$=sin(b)sin(d)sin(f)$
$\implies tan(f)=\dfrac{sin(a+b+c+d)}{\dfrac{sin(b)sin(d)}{sin(a)sin(c)}-cos(a+b+c+d)}$
When point $D$ moves outside $\triangle{ABC}$:
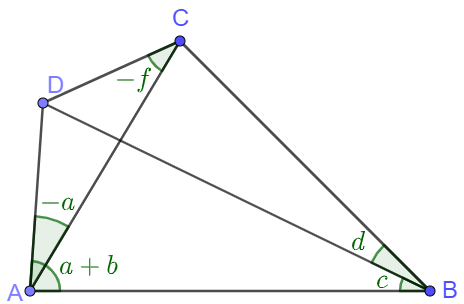
$\angle{a} \rightarrow \angle{(-a)}, \angle{f} \rightarrow \angle{(-f)}, \angle{b} \rightarrow \angle{(a+b)}$ , so above equation changes to
$tan(f)=\dfrac{sin(b+c+d)}{\dfrac{sin(a+b)sin(d)}{sin(a)sin(c)}+cos(b+c+d)}$
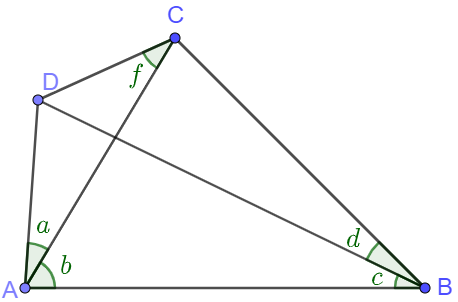
So for this problem, $\angle{a}=20^{\circ}, \angle{b}=60^{\circ}, \angle{c}=50^{\circ}, \angle{d}=30^{\circ}$
$\implies tan(f)=\dfrac{sin(140^{\circ})}{\dfrac{sin(80^{\circ})sin(30^{\circ})}{sin(20^{\circ})sin(50^{\circ})}+cos(140^{\circ})}=\dfrac{sin(40^{\circ})}{\dfrac{sin(80^{\circ})}{2sin(20^{\circ})cos(40^{\circ})}-cos(40^{\circ})}=\dfrac{sin(40^{\circ})}{\dfrac{sin(40^{\circ})}{sin(20^{\circ})}-cos(40^{\circ})}$
$=\dfrac{\dfrac{1}{2}sin(40^{\circ})}{cos(20^{\circ})-\dfrac{1}{2}cos(40^{\circ})}=\dfrac{\dfrac{1}{2}sin(40^{\circ})}{sin(70^{\circ})-sin(30^{\circ})cos(40^{\circ})}=\dfrac{\dfrac{1}{2}sin(40^{\circ})}{sin(40^{\circ}+30^{\circ})-sin(30^{\circ})cos(40^{\circ})}$
$=\dfrac{\dfrac{1}{2}sin(40^{\circ})}{sin(40^{\circ})cos(30^{\circ})+cos(40^{\circ})sin(30^{\circ})-sin(30^{\circ})cos(40^{\circ})}=\dfrac{\dfrac{1}{2}sin(40^{\circ})}{cos(30^{\circ})sin(40^{\circ})}=\dfrac{1}{\sqrt{3}}\implies \angle{f}=\bbox[1px, border: 1px solid black]{30^{\circ}}$
Reference:
05/11/2021
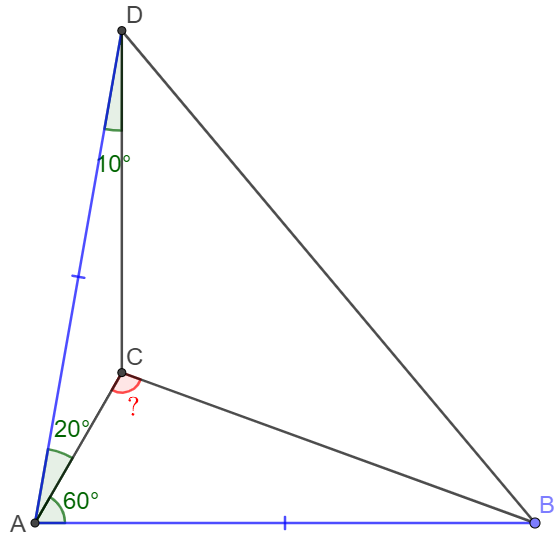
Solve:
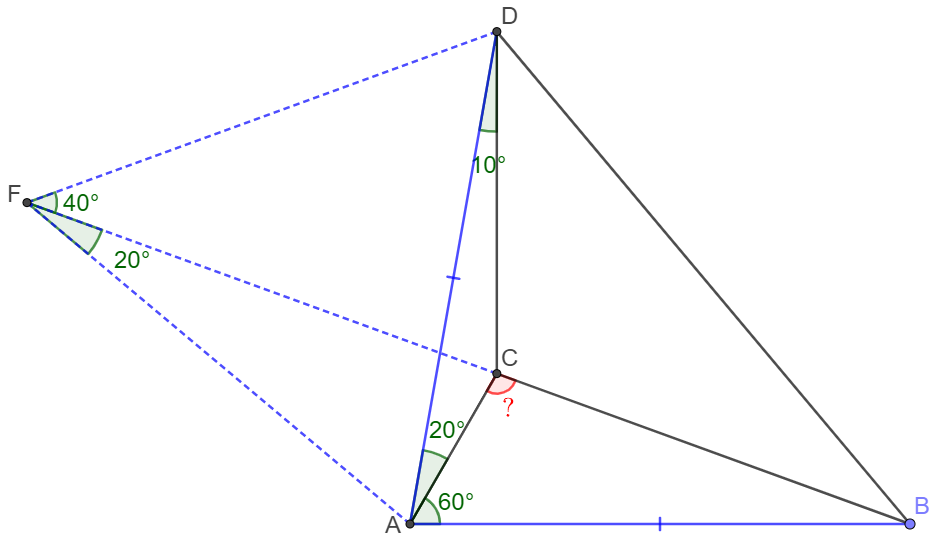
Make point $F$ to be the center of circumcenter of $\triangle{ACD}$
$\implies AF=CF=BF, \angle{CFD}=2 \cdot \angle{DAC}=40^{\circ}, \angle{AFC}=2 \cdot \angle{ADC}=20^{\circ}$
$\implies \angle{FAD}=60^{\circ}, \angle{FCA}=80^{\circ}$
We know that $AF=AD=AB$ in $\triangle{FAB}$
$ \implies \angle{AFB}=\dfrac{180^{\circ}-\angle{FAB}}{2}=\dfrac{180^{\circ}-20^{\circ}-60^{\circ}-60^{\circ}}{2}=20^{\circ}=\angle{AFC}$
$\implies F, C, B$ is collinear $\implies \angle{ACB}=180^{\circ}-80^{\circ}=\bbox[1px, border: 1px solid black]{100^{\circ}}$
05/12/2021
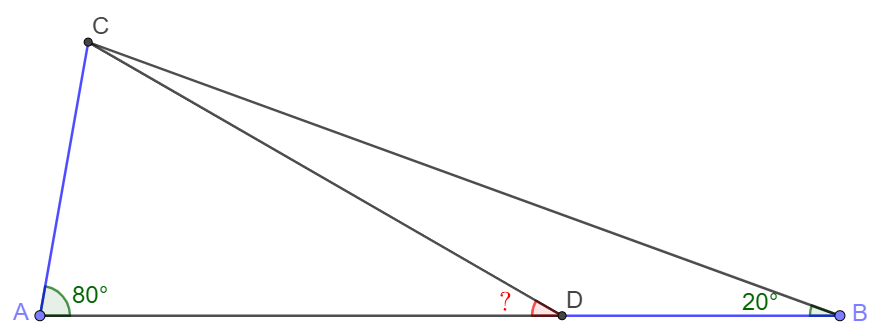
Solve:
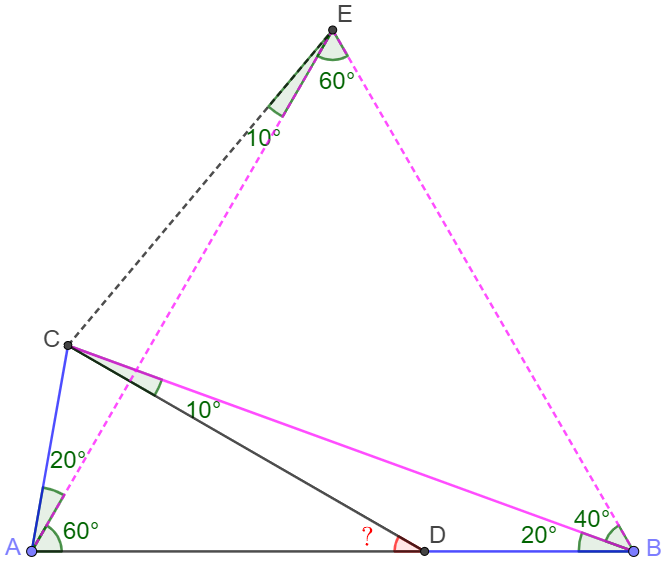
Make equilateral $\triangle{EAB}$, each to see that
$\angle{CBE}=40^{\circ}, BE=AB=BC \implies \angle{CEB}=70^{\circ} \implies \angle{CEA}=10^{\circ}$
$\angle{CAE}=\angle{DBC}=20^{\circ}, AC=BD, AE=AB=BC$
$\implies triangle{ACE} \cong \triangle{BDC} \implies \angle{DCB}=\angle{CEA}=10^{\circ}$
$\implies \angle{ADC}=\angle{DCB}+\angle{CBA}=\bbox[1px, border: 1px solid black]{30^{\circ}}$
05/13/2021
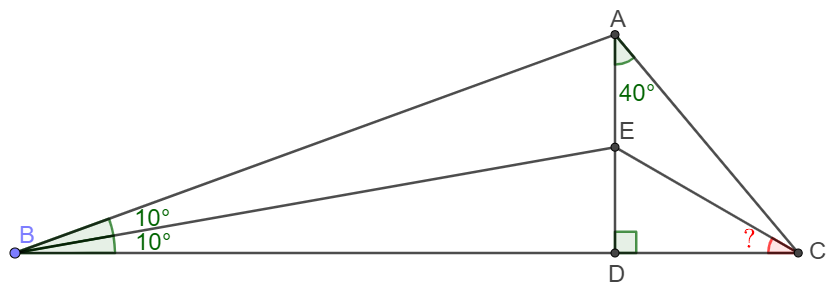
Solve 1:
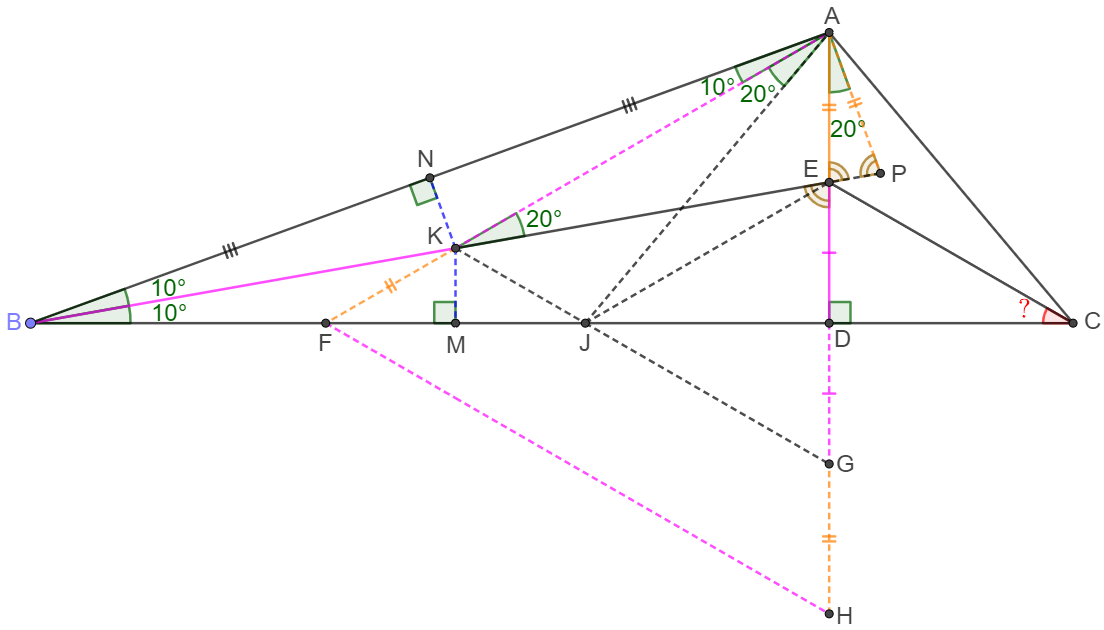
From $A$ make line $AF$ so that $\angle{BAF}=10^{\circ}$, $AF$ and $BE$ intersect at $K$, $AF$ and $BC$ intersect at $F$.
Extend $AD$ to $G$ and $H$ so that $DG=DE, AE=GH$. Connect $GK$. $GK$ and $BC$ intersect at $J$.
Easy to see that $AD=DH$, and $\angle{FAD}=60^{\circ}, AF=FH \implies \triangle{AFH}$ is equilateral triangle.
$\implies \angle{AFD}=30^{\circ} \implies \angle{FKM}=60^{\circ}$
From $K$ make $KN \perp AB, KM \perp BC$, with perpendicular foot as $N$ and $M$ perspectively.
Easy to see $KN=KM \implies KM=\dfrac{KF}{2}$
$\angle{KBA}=\angle{KAB}=10^{\circ} \implies AK=BK \implies AN=BN$
From $A$ make $\angle{EAP}=20^{\circ}$, extend $BD$ so that $BD$ and $AP$ intersect at $P$
$\angle{EBD}=10^{\circ} \implies \angle{BED}=80^{\circ} \implies \angle{AEP}=80^{\circ}=\angle{APE} \implies AE=AP$
$\implies \angle{PAB}=90^{\circ} \implies NK \parallel AP \implies AP=2NK=FK=AE=GH$
$\implies AK=AG \implies \triangle{AKG}$ is equilateral triangle $\implies \angle{AKG}=60^{\circ}$
$\implies \angle{MKJ}=60^{\circ} \implies KJ=2KM=KF=AE \implies \triangle{AKE} \cong \triangle{AKJ}, AK \parallel EJ$
$\implies \angle{KAJ}=\angle{AKE}=20^{\circ} \implies \angle{JAD}=40^{\circ} \implies \angle{JAD}=\angle{CAD}$
$\implies AJ=AC \implies JD=CD \implies \angle{ECD}=\angle{EJD}=\angle{KFM}=\bbox[1px, border: 1px solid black]{30^{\circ}}$
Solve 2:
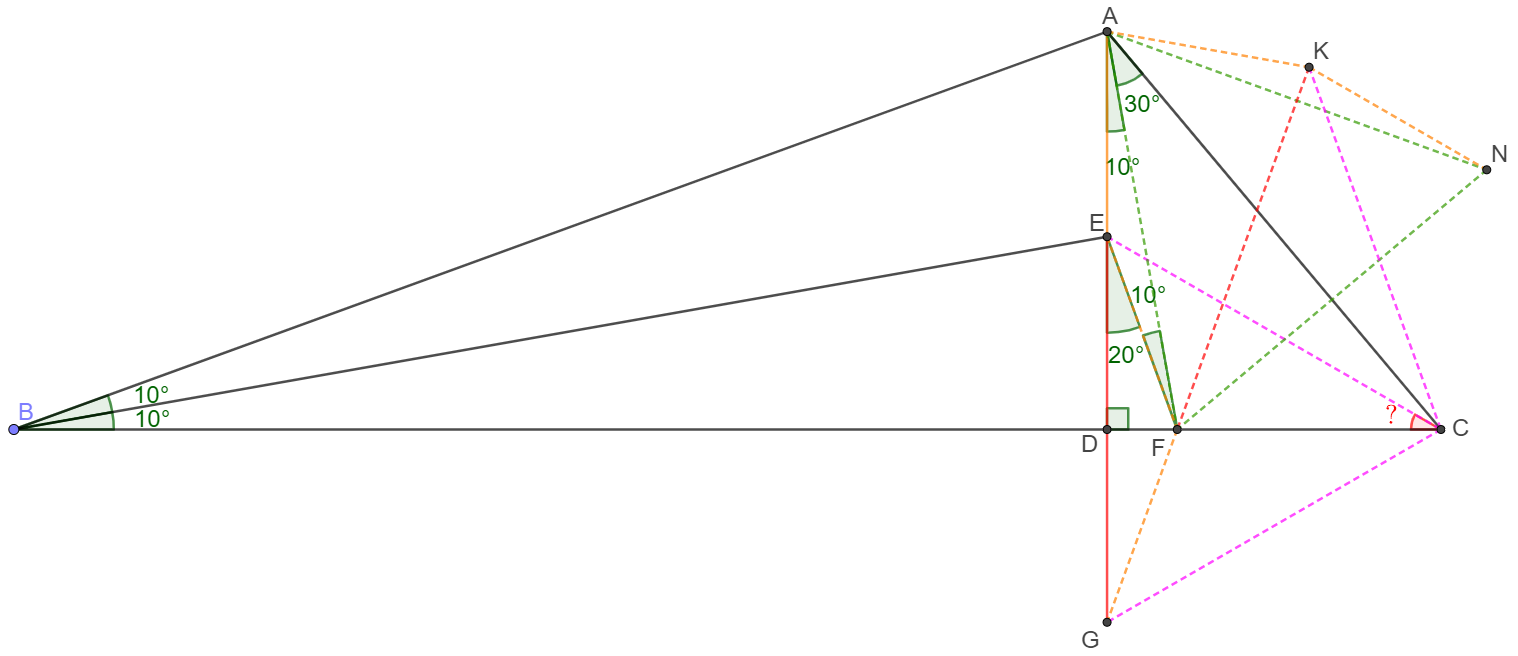
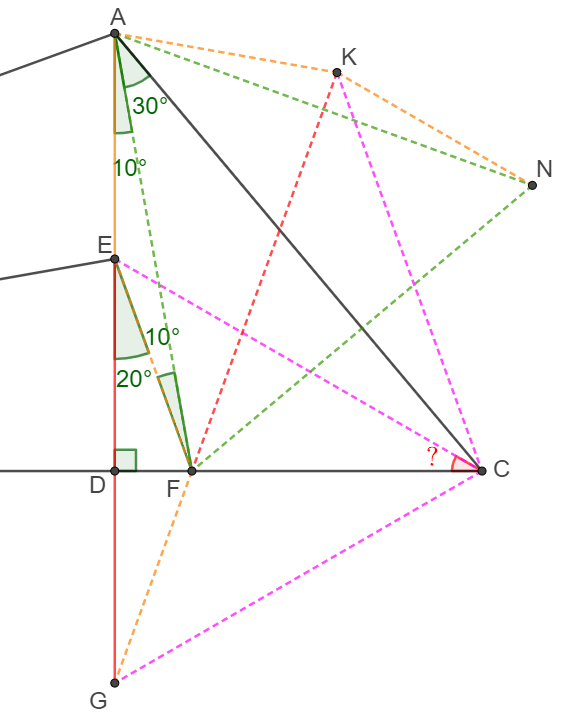
Let $F$ on CD so that $\angle{FAD}=10^{\circ}$
$\angle{BAF}=80^{\circ} \implies BA=BF \implies AE=AF \implies \angle{EFA}=10^{\circ} \implies \angle{DEF}=20^{\circ}$
Reflect $E$ across $BC$ to get $G$, reflect $E$ and $F$ across $AC$ to get $K$ and $N$.
$\angle{DEF}=20^{\circ} \implies \angle{EFG}=140^{\circ}$
$AF=AN, \angle{FAC}=\angle{CAN}=30^{\circ} \implies \triangle{AFN}$ is equilateral triangle
$AE=EF=FG=AK=KN \implies \triangle{AFK} \cong \triangle{NFK} \implies \angle{AFK}=30^{\circ}$
$\implies \angle{EFG}+\angle{EFA}+\angle{AFK}=140^{\circ}+10^{\circ}+30^{\circ}=180^{\circ} \implies GFK$ are collinear
And we know $CG=CE=CK, \angle{GCK}=2 \cdot \angle{BCA}=100^{\circ}$
$\implies \angle{CGF}=\dfrac{180^{\circ}-100^{\circ}}{2}=40^{\circ} \implies \angle{FEC}=40^{\circ} \implies \angle{ECD}=90^{\circ}-20^{\circ}-40^{\circ}=\bbox[1px, border: 1px solid black]{30^{\circ}}$
Solve 3:
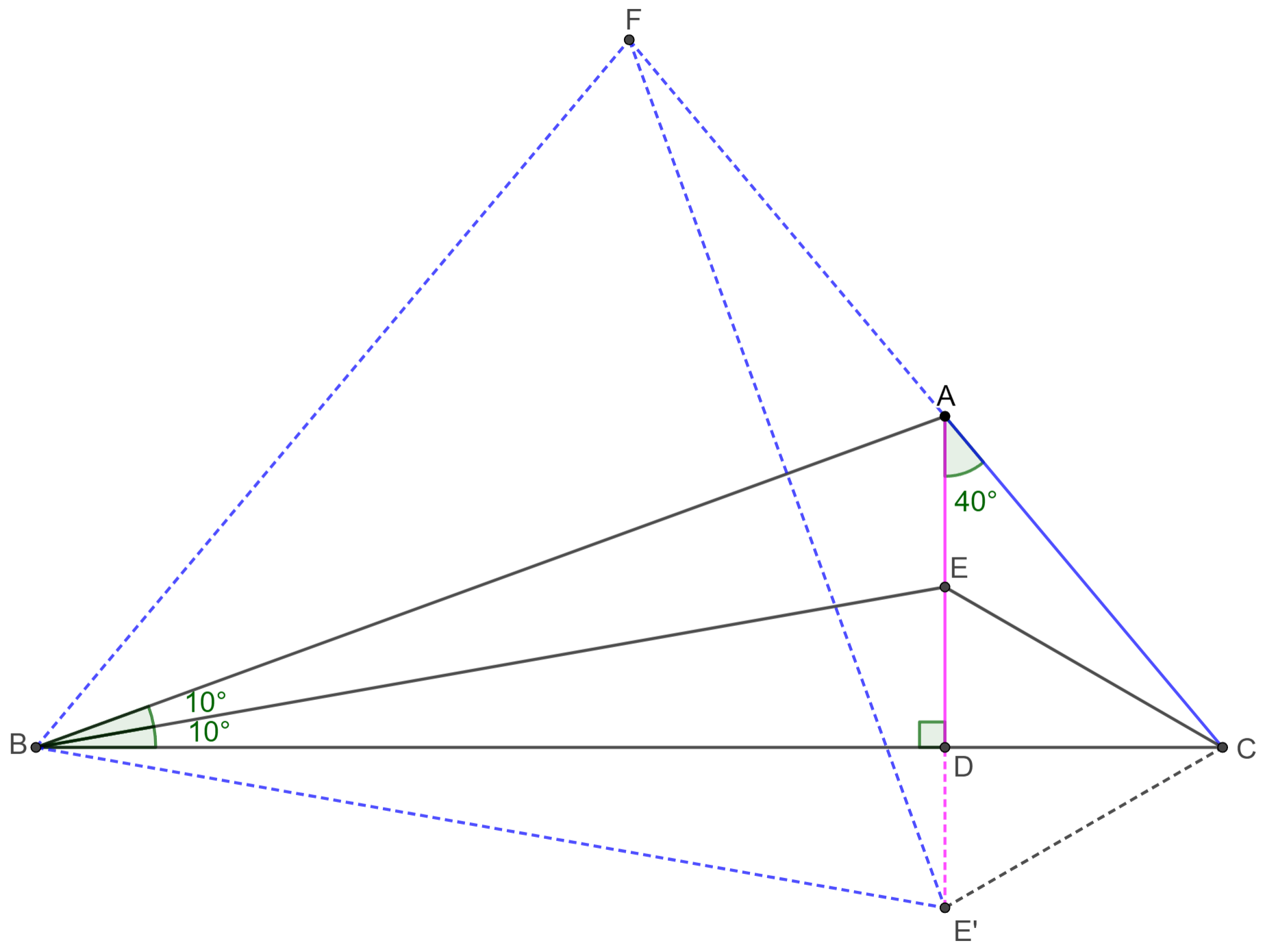 \(\begin{multline}\nonumber
\shoveleft \text{Let } E' \text{ be the mirror point of } E \text{ along line } BC, \text{ and make equilateral triangle } \triangle{BE'F}\\
\shoveleft \text{ with } F \text{ on the same side of } BC \text{ as point } A. \text{Connect } AF.\\
\shoveleft \text{Easy to see } \angle{ABE'}=30^{\circ} \implies \angle{ABF}=30^{\circ}, AB \perp E'F, AE'=AF\\
\shoveleft \implies \angle{BAF}=\angle{BAE'}=70^{\circ} \implies \angle{E'AF}=140^{\circ}, \angle{AE'F}=\angle{AFE'}=20^{\circ}\\
\shoveleft \implies \angle{FAC}=140^{\circ}+40^{\circ}=180^{\circ} \implies C,A,F \text{ are colinear } \implies CF=AB=AE'\\
\shoveleft \implies \angle{FCE'}=80^{\circ}\implies \angle{E'CD}=80^{\circ}-50^{\circ}=30^{\circ}\implies \angle{BCE}=\angle{E'CD}=\bbox[5px, border: 1px solid black]{30^{\circ}}
\end{multline}\)
\(\begin{multline}\nonumber
\shoveleft \text{Let } E' \text{ be the mirror point of } E \text{ along line } BC, \text{ and make equilateral triangle } \triangle{BE'F}\\
\shoveleft \text{ with } F \text{ on the same side of } BC \text{ as point } A. \text{Connect } AF.\\
\shoveleft \text{Easy to see } \angle{ABE'}=30^{\circ} \implies \angle{ABF}=30^{\circ}, AB \perp E'F, AE'=AF\\
\shoveleft \implies \angle{BAF}=\angle{BAE'}=70^{\circ} \implies \angle{E'AF}=140^{\circ}, \angle{AE'F}=\angle{AFE'}=20^{\circ}\\
\shoveleft \implies \angle{FAC}=140^{\circ}+40^{\circ}=180^{\circ} \implies C,A,F \text{ are colinear } \implies CF=AB=AE'\\
\shoveleft \implies \angle{FCE'}=80^{\circ}\implies \angle{E'CD}=80^{\circ}-50^{\circ}=30^{\circ}\implies \angle{BCE}=\angle{E'CD}=\bbox[5px, border: 1px solid black]{30^{\circ}}
\end{multline}\)
Solve 4:
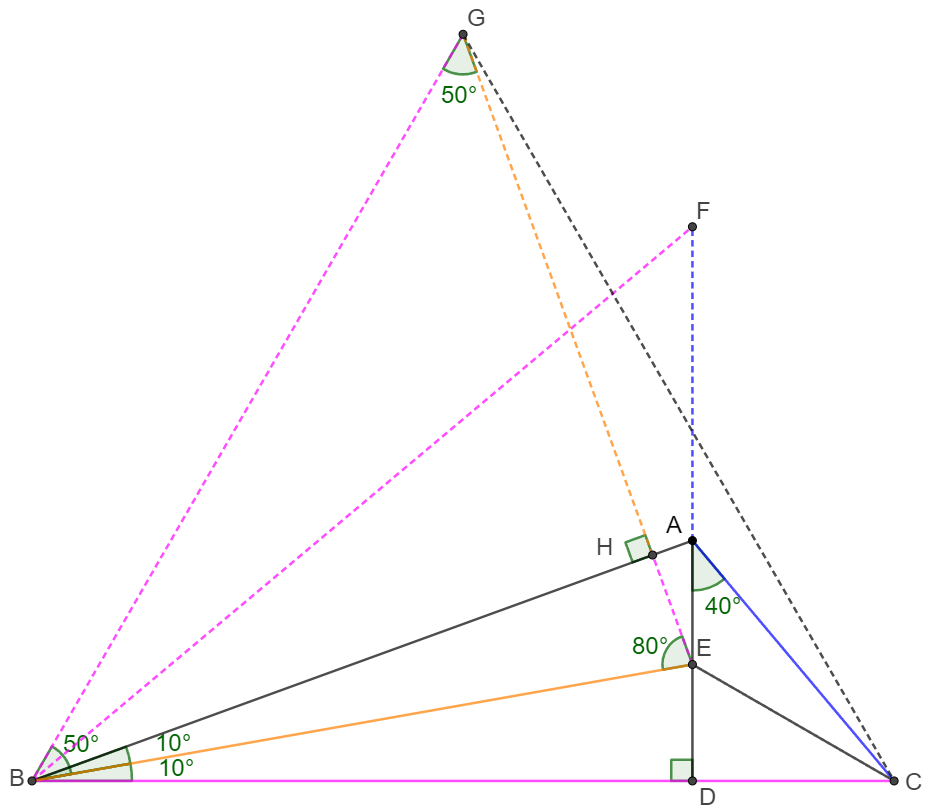 \(\begin{multline}\nonumber
\shoveleft \text{Extend } DA \text{ to } F \text{ such that } AC=AF \implies \angle{BAF}=180^{\circ}-\angle{BAD}=110^{\circ}=\angle{BAC}\\
\shoveleft \implies \triangle{BAC} \cong \triangle{BAF} \implies BC=BF, \angle{BFA}=\angle{BCA}=50^{\circ}\\
\shoveleft \text{Make } EG \perp AB, EG=EB, EG \text{ and } AB \text{ intersect at } H, \angle{BEG}=80^{\circ}\\
\shoveleft \implies \angle{EBG}=\angle{EGB}=50^{\circ}, \triangle{BDE} \cong \triangle{BDH} \implies BH=BD\\
\shoveleft \implies \triangle{BDF} \cong \triangle{BHG} \implies BG=BF=BC, \angle{CBG}=60^{\circ} \implies \triangle{BCG} \text{ is equilateral}\\
\shoveleft \implies BC=CG \implies \triangle{BCE} \cong \triangle{GCE} \implies \angle{BCE}=\angle{GCE}=\bbox[5px, border: 1px solid black]{30^{\circ}}
\end{multline}\)
\(\begin{multline}\nonumber
\shoveleft \text{Extend } DA \text{ to } F \text{ such that } AC=AF \implies \angle{BAF}=180^{\circ}-\angle{BAD}=110^{\circ}=\angle{BAC}\\
\shoveleft \implies \triangle{BAC} \cong \triangle{BAF} \implies BC=BF, \angle{BFA}=\angle{BCA}=50^{\circ}\\
\shoveleft \text{Make } EG \perp AB, EG=EB, EG \text{ and } AB \text{ intersect at } H, \angle{BEG}=80^{\circ}\\
\shoveleft \implies \angle{EBG}=\angle{EGB}=50^{\circ}, \triangle{BDE} \cong \triangle{BDH} \implies BH=BD\\
\shoveleft \implies \triangle{BDF} \cong \triangle{BHG} \implies BG=BF=BC, \angle{CBG}=60^{\circ} \implies \triangle{BCG} \text{ is equilateral}\\
\shoveleft \implies BC=CG \implies \triangle{BCE} \cong \triangle{GCE} \implies \angle{BCE}=\angle{GCE}=\bbox[5px, border: 1px solid black]{30^{\circ}}
\end{multline}\)
Solve 5:
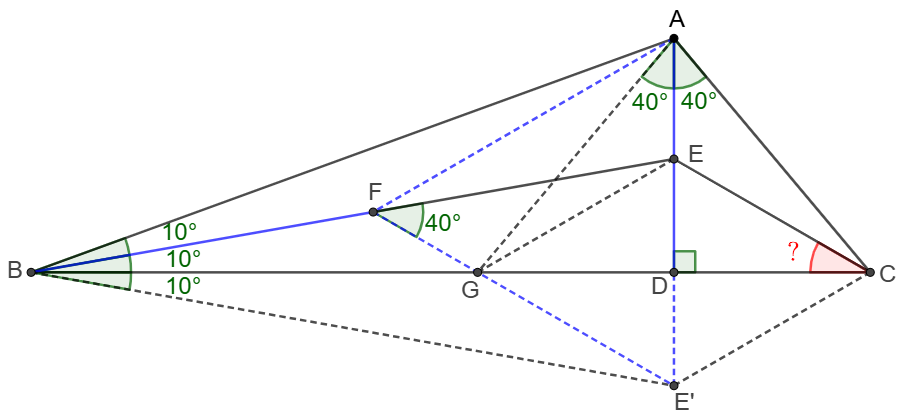 \(\begin{multline}
\shoveleft \text{Let }E' \text{ be the reflection of }E \text{ along }BC \implies \angle{E'BD}=\angle{DBE}=10^{\circ}\\
\shoveleft \text{Let }F \text{ be the circumcenter of }\triangle{ABE'} \implies \angle{AFE'}=2\angle{ABE'}=60^{\circ} \\
\shoveleft \implies \triangle{AE'F} \text{ is equilateral }\implies AF=BF=E'F=AE'\\
\shoveleft \angle{AE'F}=60^{\circ} \implies \angle{FE'B}=20^{\circ}=\angle{FBE'} \implies F \text{ is on }BE\\
\shoveleft \text{Let }E'F\cap BD=G, \angle{E'GD}=30^{\circ}=\angle{EGD}\implies \angle{EGE'}=60^{\circ}=\angle{FAE'}\\
\shoveleft \implies AFGE \text{ is cyclic} \implies \angle{EFE'}=40^{\circ}=\angle{GAE'}=\angle{CAE'}\\
\shoveleft \implies \triangle{AGD}\cong\triangle{ACD}\implies AG=AC\implies \triangle{AE'G}\cong\triangle{AE'C}\\
\shoveleft \implies E'G=E'C\implies \angle{E'GD}=\angle{E'CD}=\angle{ECD}=\bbox[5px, border: 1px solid black]{30^{\circ}}\\
\end{multline}\)
\(\begin{multline}
\shoveleft \text{Let }E' \text{ be the reflection of }E \text{ along }BC \implies \angle{E'BD}=\angle{DBE}=10^{\circ}\\
\shoveleft \text{Let }F \text{ be the circumcenter of }\triangle{ABE'} \implies \angle{AFE'}=2\angle{ABE'}=60^{\circ} \\
\shoveleft \implies \triangle{AE'F} \text{ is equilateral }\implies AF=BF=E'F=AE'\\
\shoveleft \angle{AE'F}=60^{\circ} \implies \angle{FE'B}=20^{\circ}=\angle{FBE'} \implies F \text{ is on }BE\\
\shoveleft \text{Let }E'F\cap BD=G, \angle{E'GD}=30^{\circ}=\angle{EGD}\implies \angle{EGE'}=60^{\circ}=\angle{FAE'}\\
\shoveleft \implies AFGE \text{ is cyclic} \implies \angle{EFE'}=40^{\circ}=\angle{GAE'}=\angle{CAE'}\\
\shoveleft \implies \triangle{AGD}\cong\triangle{ACD}\implies AG=AC\implies \triangle{AE'G}\cong\triangle{AE'C}\\
\shoveleft \implies E'G=E'C\implies \angle{E'GD}=\angle{E'CD}=\angle{ECD}=\bbox[5px, border: 1px solid black]{30^{\circ}}\\
\end{multline}\)
05/14/2021
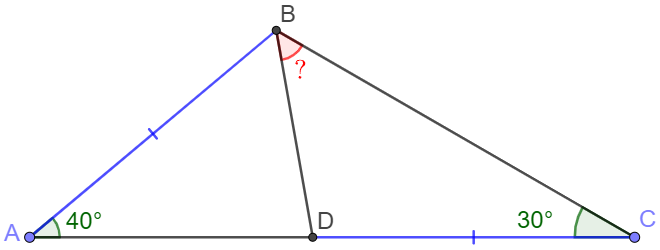
Solve:
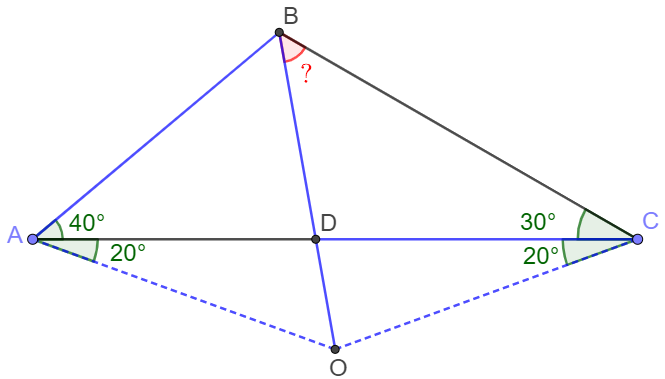
Let $O$ be the circumcenter of $\triangle{ABC} \implies AO=BO=CO$
$\angle{ACB}=30^{\circ} \implies \angle{AOB}=60^{\circ} \implies \triangle{AOB}$ is equilateral triangle
$\implies AO=AB=CD=CO, \angle{OAD}=20^{\circ} \implies \angle{OCD}=20^{\circ}$
$\implies \angle{COD}=80^{\circ} \implies \angle{DOA}=180^{\circ}-20^{\circ}-20^{\circ}-80^{\circ}=60^{\circ}=\angle{BOA}$
$\implies BDO$ are collinear, thus
$BO=CO \implies \angle{CBO}=\angle{OCB}=\angle{OCD}+\angle{DCB}=50^{\circ}$
$\implies \angle{CBD}=\angle{CBO}=\bbox[1px, border: 1px solid black]{50^{\circ}}$
05/15/2021
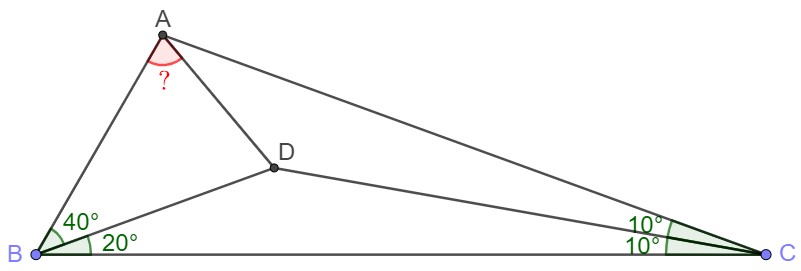
Solve:
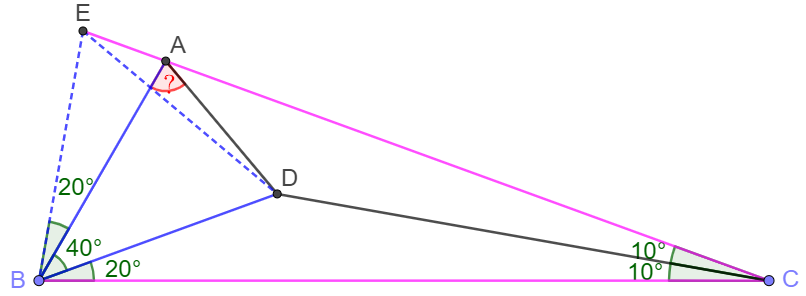
Extend $CA$ to $E$ so that $\angle{EBA}=20^{\circ}$.
Easy to see that $\angle{EBC}=\angle{BEC}=80^{\circ} \implies BC=EC$
$\implies \triangle{ECD} \cong \triangle{BCD} \implies \angle{CED}=\angle{CBD}=20^{\circ}, BD=ED$
$\angle{BEC}=80^{\circ} \implies \angle{BEC}=\angle{BAE} \implies BE=BA$
$\angle{EBD=60^{\circ}, BE=BA \implies \triangle{BDE}}$ is equilateral triangle
$\implies BE=BD \implies AB=BD \implies \angle{BAD}=\dfrac{180^{\circ}-40^{\circ}}{2}=\bbox[1px, border: 1px solid black]{70^{\circ}}$
05/16/2021
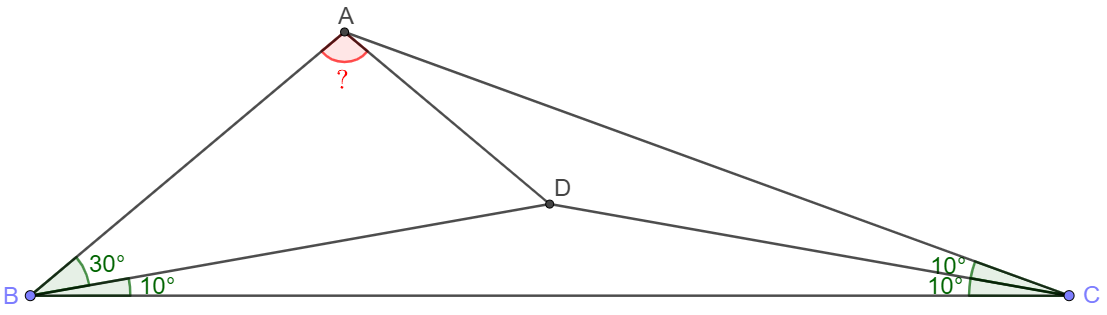
Solve:
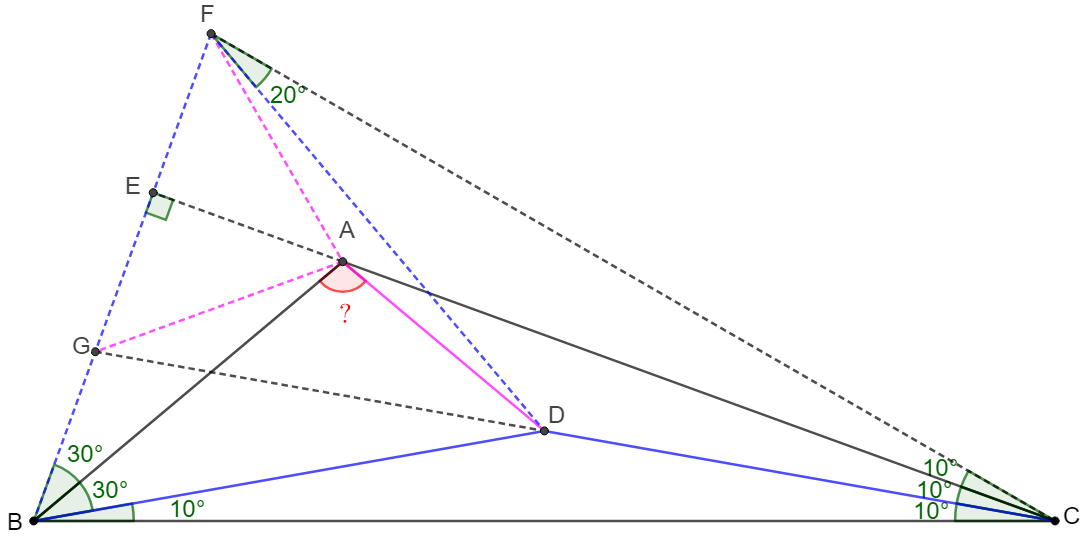 .
\(\begin{multline}\nonumber
\shoveleft \text{Make equilateral triangle }\triangle{BDF} \text{ on the same side of } BC \text{ as }A.\\
\shoveleft \text{Connect } CF, \text{ extend } CD, CA \text{ and intersect with } BF \text{ at }G, E.\\
\shoveleft \text{Connect } AD, AF, AG. \text{Easy to see } AC \perp BC \implies \angle{EGC}=80^{\circ}\\
\shoveleft BD=FD=CD \implies \angle{DFC}=\angle{DCF}=20^{\circ}\\
\shoveleft \implies\angle{ACF}=10^{\circ}=\angle{ACG} \implies \triangle{CEG}\cong\triangle{CEF}\\
\shoveleft \implies CF=CG\implies \triangle{CAG}\cong\triangle{CAF}\implies AF=AG\\
\shoveleft \triangle{ABD}=30^{\circ}=\angle{ABF}, BD=BF\implies \triangle{ABD}\cong\triangle{ABF}\\
\shoveleft \implies AD=AF=AG \implies A \text{ is the circumcenter of }\triangle{DGF}\\
\shoveleft \implies \angle{FAD}=2\angle{EGC}=160^{\circ}\implies \angle{AFB}=\angle{ABF}=10^{\circ}=\angle{ACD}\\
\shoveleft \implies CDAF \text{ is cyclic }\implies \angle{DAC}=\angle{DFC}=20^{\circ}\implies \angle{BAD}=\bbox[5px, border:1px solid black]{100^{\circ}}
\end{multline}\)
.
\(\begin{multline}\nonumber
\shoveleft \text{Make equilateral triangle }\triangle{BDF} \text{ on the same side of } BC \text{ as }A.\\
\shoveleft \text{Connect } CF, \text{ extend } CD, CA \text{ and intersect with } BF \text{ at }G, E.\\
\shoveleft \text{Connect } AD, AF, AG. \text{Easy to see } AC \perp BC \implies \angle{EGC}=80^{\circ}\\
\shoveleft BD=FD=CD \implies \angle{DFC}=\angle{DCF}=20^{\circ}\\
\shoveleft \implies\angle{ACF}=10^{\circ}=\angle{ACG} \implies \triangle{CEG}\cong\triangle{CEF}\\
\shoveleft \implies CF=CG\implies \triangle{CAG}\cong\triangle{CAF}\implies AF=AG\\
\shoveleft \triangle{ABD}=30^{\circ}=\angle{ABF}, BD=BF\implies \triangle{ABD}\cong\triangle{ABF}\\
\shoveleft \implies AD=AF=AG \implies A \text{ is the circumcenter of }\triangle{DGF}\\
\shoveleft \implies \angle{FAD}=2\angle{EGC}=160^{\circ}\implies \angle{AFB}=\angle{ABF}=10^{\circ}=\angle{ACD}\\
\shoveleft \implies CDAF \text{ is cyclic }\implies \angle{DAC}=\angle{DFC}=20^{\circ}\implies \angle{BAD}=\bbox[5px, border:1px solid black]{100^{\circ}}
\end{multline}\)
05/17/2021
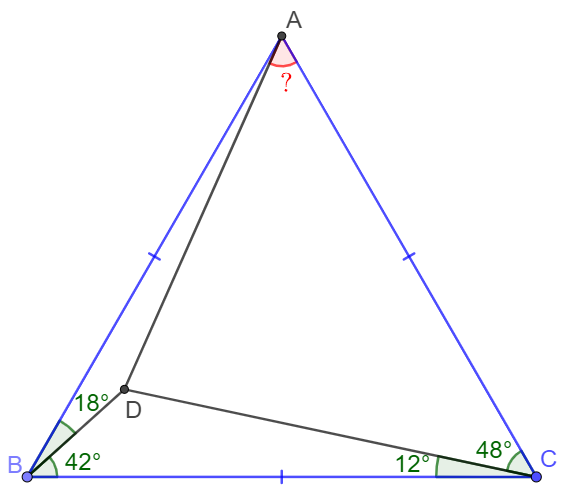
Solve:
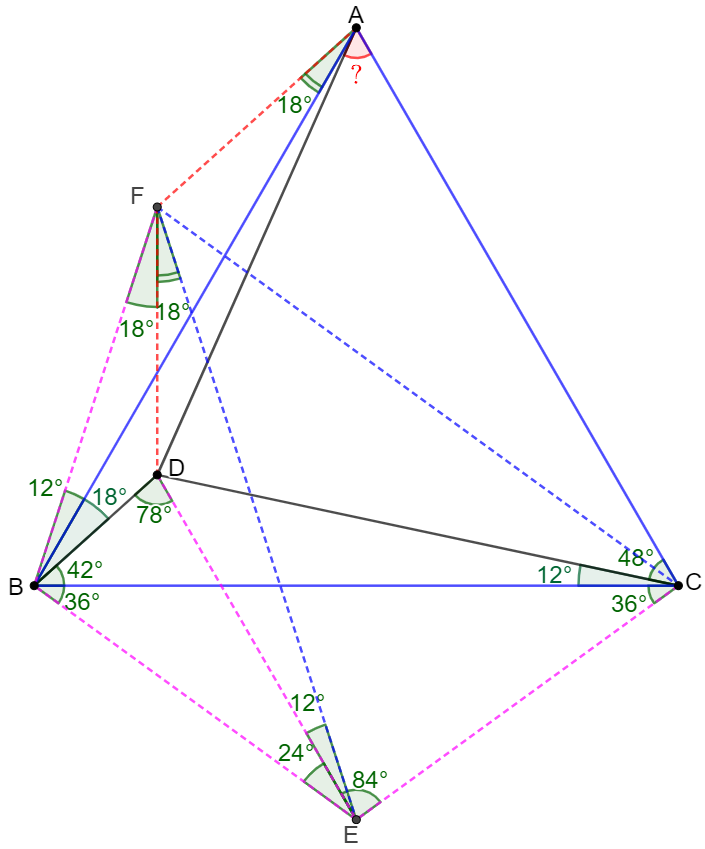
Solve: . \(\begin{multline}\nonumber \shoveleft \text{Let } E \text{ be the circumcenter of } \triangle{BCD}, \text{ so } BE=CE=DE, \angle{BED}=2\angle{BCD}=2*12^{\circ}=24^{\circ}\\ \shoveleft \implies \angle{EBD}=\angle{BDE}=\dfrac{180^{\circ}-24^{\circ}}{2}=78^{\circ}\\ \shoveleft \implies \angle{EBC}=\angle{ECB}=78^{\circ}-42^{\circ}=36^{\circ}\\ \shoveleft \implies \angle{BEC}=108^{\circ}\\ \shoveleft \text{Find } F \text{ such that } BE=BF=CE=DE, \angle{FBE}=108^{\circ}, \text{ connect } AF, CF, DF, EF. \text{ So we know that}\\ \shoveleft \text{(1) }\angle{FBC}=108^{\circ}-36^{\circ}=72^{\circ}\\ \shoveleft \text{(2) }\triangle{BCE} \cong \triangle{BEF} \implies EF=BC=AB, \angle{BFE}=\angle{BEF}=36^{\circ}=\angle{BCE}=\angle{EBC}\\ \shoveleft \implies \angle{DEF}=36^{\circ}-24^{\circ}=12^{\circ}\\ \shoveleft \text{(3) }\angle{ABF}=108^{\circ}-78^{\circ}-18^{\circ}=12^{\circ}=\angle{DEF}\\ \shoveleft \implies \triangle{ABF} \cong \triangle{FED} \text{ [SAS]}\\ \shoveleft \implies AF=DF, \angle{FAB}=\angle{DFE}\\ \shoveleft \implies \angle{FDA}=\angle{FAD}\\ \shoveleft \angle{BFE}=\angle{BCE} \implies BECF \text{ are cyclic}\\ \shoveleft \implies \angle{FCB}=\angle{BEF}=36^{\circ}\\ \shoveleft \implies \angle{BFC}=180^{\circ}-\angle{FCB}-\angle{FBC}=72^{\circ}=\angle{FBC}\\ \shoveleft \implies BC=FC=AC\\ \shoveleft \implies \text{C is circumcenter of } \triangle{ABF}\\ \shoveleft \implies \angle{AFB}=180^{\circ}-\dfrac{\angle{ACB}}{2}=180^{\circ}-30^{\circ}=150^{\circ}\\ \shoveleft \implies \angle{FAB}=\angle{DFE}=180^{\circ}-150^{\circ}-12^{\circ}=18^{\circ}\\ \shoveleft \implies \angle{BFD}=36^{\circ}-18^{\circ}=18^{\circ}\\ \shoveleft \implies \angle{DFA}=150^{\circ}-18^{\circ}=132^{\circ}\\ \shoveleft \implies \angle{FDA}=\angle{FAD}=\dfrac{180^{\circ}-132^{\circ}}{2}=24^{\circ}\\ \shoveleft \implies \angle{BAD}=\angle{FAD}-\angle{FAB}=24^{\circ}-18^{\circ}=6^{\circ}\\ \shoveleft \implies \angle{DAC}=\angle{BAC}-\angle{BAD}=60^{\circ}-6^{\circ}=\bbox[1px, border: 1px solid black]{54^{\circ}}\\ \end{multline}\)