04/01/2021
In $\triangle{ABC}, \angle{ABC}=30^{\circ}, \angle{ACB}=40^{\circ}$, $D$ is on $BC$ so that $AC=BD$, Find $\angle{DAC}$.
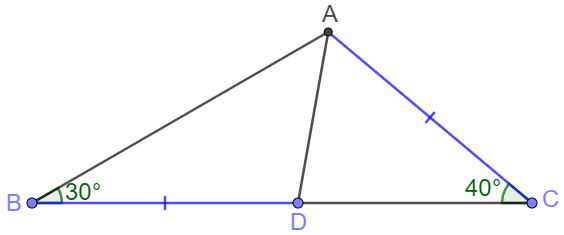
Solve:
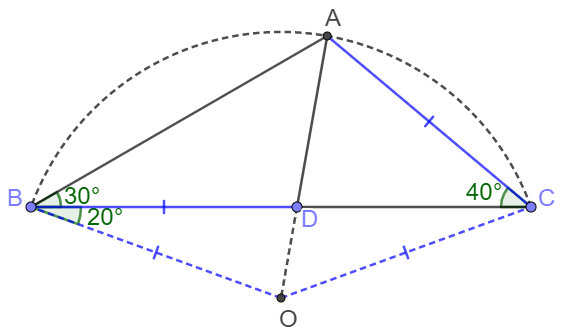
\(\begin{multline} \shoveleft \text{Make the circum-circle of } \triangle{ABC} \text{ and let its center to be } O\\ \shoveleft \angle{ABC}=30^{\circ} \implies \angle{AOC}=60^{\circ}, AC=OC \implies \angle{OCB}=20^{\circ} \\ \shoveleft BO=CO \implies \angle{OBC}=20^{\circ}, BD=AC=CO=BO\\ \shoveleft \text{Connect }DO, \text{ easy to see that }\angle{BOD}=\angle{BDO}=80^{\circ}\\ \shoveleft \angle{DOC}=180^{\circ}-\angle{OBC}-\angle{OCB}-\angle{BOD}\\ \shoveleft =180^{\circ}-20^{\circ}-20^{\circ}-80^{\circ}=60^{\circ}=\angle{AOC}\\ \shoveleft \implies O, D, A \text{ collinear }\implies \angle{DAC}=\angle{OAC}=\bbox[1px, border: 1px solid black]{60^{\circ}} \end{multline}\) —
04/02/2021
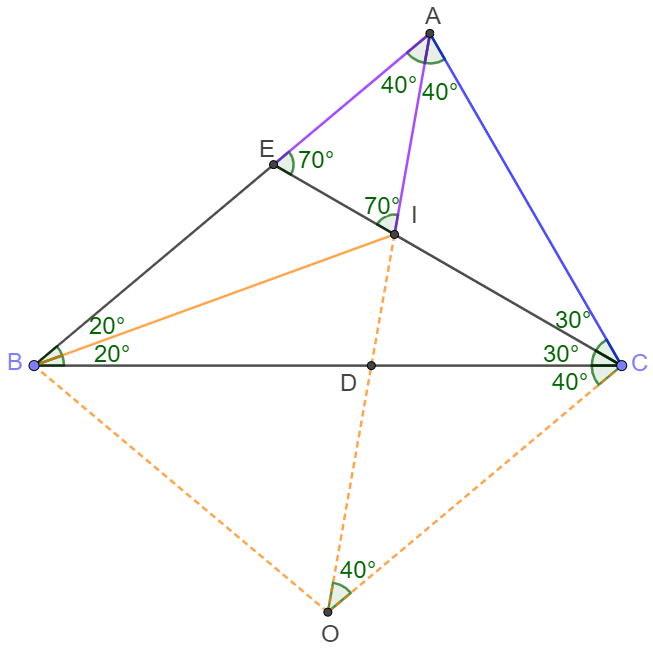
In $\triangle{ABC}, \angle{ABC}=40^{\circ}, \angle{BAC}=80^{\circ}, \angle{ACB}=60^{\circ}$, $I$ is the in-center. Prove:
(1) $BI=AC; $ (2) $CD+AD=AC+AE;$ (3) $2AC=CD+AB$
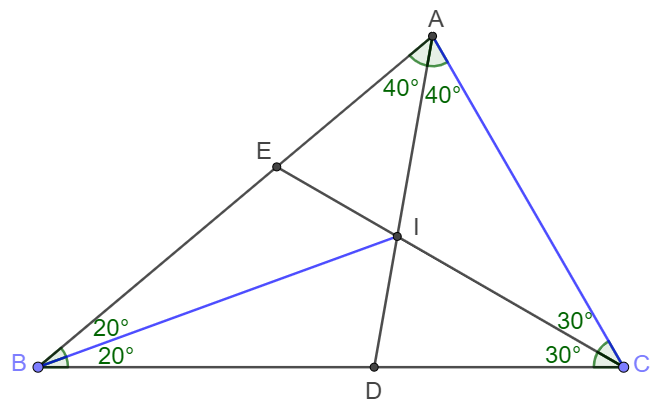
Prove:
(1) Let $D$ be the center of circumcircle of $\triangle{BIC} \implies OB=OI=OC$
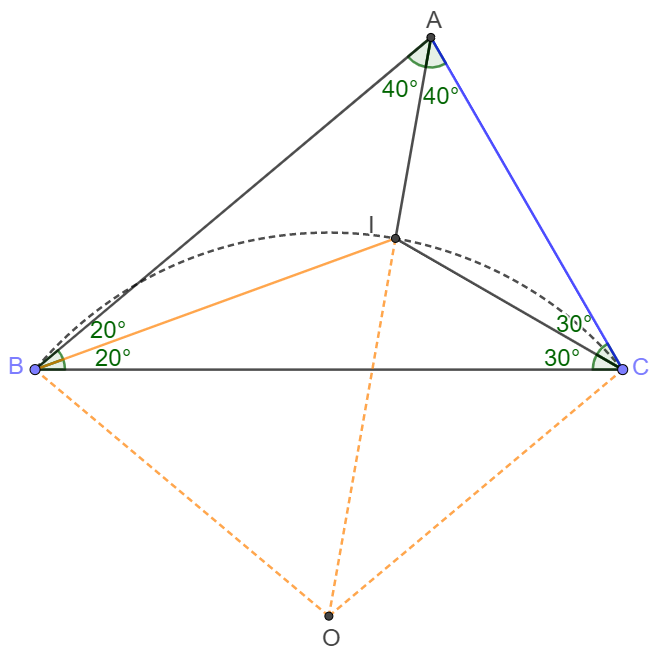
$\angle{BCI}=30^{\circ} \implies \angle{BOI}=60^{\circ} \implies \triangle{BOI} $ is equilateral
$\implies \angle{OBI}=60^{\circ} \implies \angle{OBC}=40^{\circ} \implies \angle{OCB}=40^{\circ}$
$\implies \angle{OCI}=70^{\circ} \implies \angle{COI}=180^{\circ}-2*\angle{OCI}=40^{\circ}$
$\implies \angle{COI}+\angle{OCB}+\angle{ACB}+\angle{CAI}=40^{\circ}+40^{\circ}+60^{\circ}+40^{\circ}=180^{\circ}$
$\implies A, I, O $ is collinear $\implies \angle{COA}=\angle{OAC}=40^{\circ} \implies AC=CO=BI \blacksquare$
(2) Easy to know from (1) that $\angle{AEI}=\angle{AIE}=70^{\circ} \implies AE=AI$
Also $\angle{AOC}=\angle{BCO}=40^{\circ} \implies CD=OD$
So $AD+DC=AD+DO=AO=AI+OI=AE+AC\blacksquare$
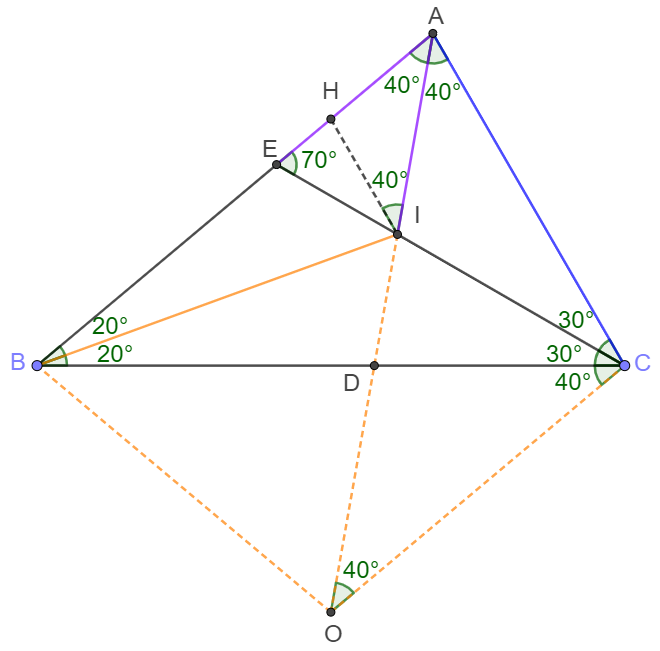
(3) Let $I$ be on $AE$ so that $\angle{AIH}=40^{\circ} \implies AH=HI$
$\angle{AIE}=70^{\circ} \implies \angle{HIE}=30^{\circ}$
$\implies \angle{AHI}=80^{\circ}=\angle{BIH}=\angle{BIE}+\angle{HIE}=80^{\circ}$
$\implies BH=BI \implies AB=BI+DI $
$\implies AC=AB-DI $
$\implies 2AC=AC-DI+AB=OI-DI+AB=OD+AB=CD+AB\blacksquare$
04/02/2021
In $\triangle{ABC}, \angle{ABC}=15^{\circ}, ACB=30^{\circ},$ $D$ is midpoint of $BC$. Find $\angle{DAB}$.
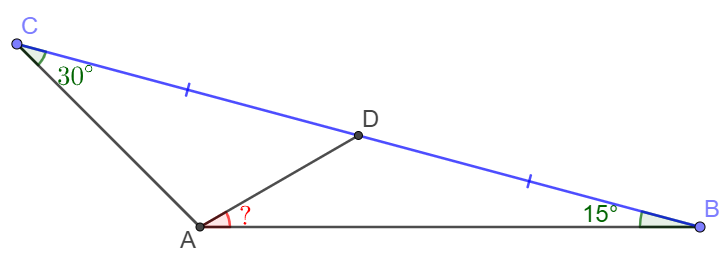
Solve:
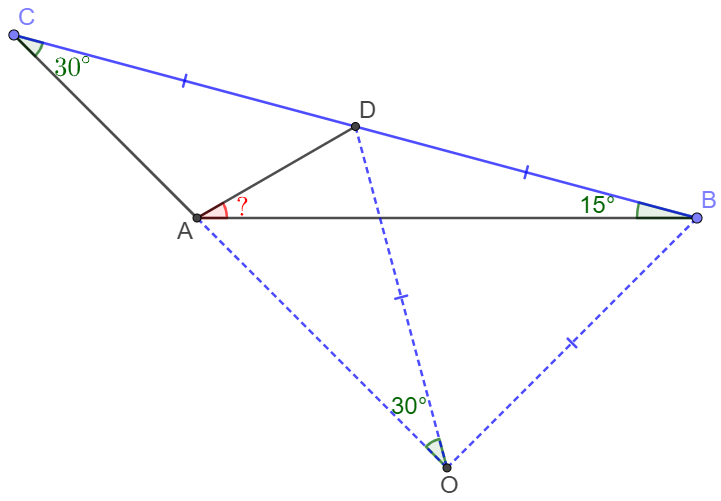
Extend $CA$ to $O$ so that $\angle{AOD}=30^{\circ} \implies CD=OD=DB$
And $\angle{ODB}=60^{\circ} \implies \triangle{ODB}$ is equilateral
$\implies \angle{DBO}=\angle{DOB}=60^{\circ} \implies \angle{ABO}=45^{\circ}, \angle{AOB}=90^{\circ}$
$\implies \angle{OAB}=180^{\circ}-90^{\circ}-45^{\circ}=45^{\circ} \implies \angle{OAB}=\angle{ABO}$
$\implies AO=BO=DO \implies \angle{DAO}=75^{\circ}$
$\implies \angle{DAB}=75^{\circ}-45^{\circ}=\bbox[1px, border: 1px solid black]{30^{\circ}}$
04/05/2021
Let $ABC$ be a triangle and $X$ an interior point of $\triangle{ABC}$. Show that at least one of the angles $\angle{XAB}, \angle{XBC}, \angle{XCA}$ is less than or equal to $30^{\circ}$. IMO 1991 B2
Prove: \(\begin{multline} \shoveleft \text{Prove by contradiction: if none of the angles }\angle{XAB}, \angle{XBC}, \angle{XCA} \text{ is less than or equal to }30^{\circ} \text{, then}\\ \shoveleft \angle{XAB} + \angle{XBC} + \angle{XCA} > 90^{\circ} \implies \angle{XAC} + \angle{XCB} + \angle{XBA} < 90^{\circ}\\ \shoveleft sin(\angle{XAB}) > \dfrac{1}{2}, sin(\angle{XBC}) > \dfrac{1}{2}, sin(\angle{XCA}) > \dfrac{1}{2} \implies sin(\angle{XAB}) \cdot sin(\angle{XBC}) \cdot sin(\angle{XCA}) > \dfrac{1}{8} \\ \shoveleft \text{ From }\href{https://www.cut-the-knot.org/triangle/TrigCeva.shtml}{\text{Trigonometric Form of Ceva's Theorem}} \text{ we know} \\ \shoveleft sin(\angle{XAB}) \cdot sin(\angle{XBC}) \cdot sin(\angle{XCA}) = sin(\angle{XAC}) \cdot sin(\angle{XCB}) \cdot sin(\angle{XBA})\\ \shoveleft \implies sin(\angle{XAC}) \cdot sin(\angle{XCB}) \cdot sin(\angle{XBA}) > \dfrac{1}{8}\text{where } \angle{XAC} + \angle{XCB} + \angle{XBA} < 90^{\circ} \\ \shoveleft \text{Let }x=\angle{XAC}, y=\angle{XCB}, z=\angle{XAC} \implies 0 < z < 90^{\circ} - x - y \implies 0 < sin(z) < sin(90^{\circ} - x - y) = cos(x + y) \\ \shoveleft \implies sin(x) \cdot sin(y) \cdot cos(x + y) > sin(x) \cdot sin(y) \cdot sin(z) > \dfrac{1}{8} \text{ where }0 < x + y < 90^{\circ}\\ \shoveleft \implies \dfrac{1}{2}(cos(x-y) - cos(x+y))cos(x + y) > \dfrac{1}{8} \implies 4(cos(x-y) - cos(x+y))cos(x + y) > 1\\ \shoveleft \text{Obviously } 1 \ge cos(x-y) \implies 4(1 - cos(x + y))cos(x + y) \ge 4(cos(x - y)-cos(x+y))cos(x + y) > 1\\ \shoveleft \implies 4(cos(x + y) - 1)cos(x + y) +1 < 0 \implies (2cos(x+ y)-1)^2 < 0\\ \shoveleft \text{This is impossible. So we know the assumption is not correct.}\blacksquare \\ \shoveleft \text{Above analysis means that, for }sin(x)sin(y)cos(x+y), 0 < x + y < \dfrac{\pi}{2} \text{, it gets maximum value when }\\ \shoveleft cos(x-y)=0 \implies x=y \text{ and }(2cos(x+y) - 1)^2=0 \implies cos(x+y)=\dfrac{1}{2} \implies x=y=\dfrac{\pi}{6}\\ \shoveleft \text{We can verify this by }\href{https://www.wolframalpha.com/input/?i=findmaximum%5Bsin%28x%29*sin%28y%29*cos%28x%2By%29%2C+0%3Cx%2By%3Cpi%2F2%5D}{Wolfram}: \\ \shoveleft max \bigg \{ sin(x)sin(y)cos(x+y) \bigg \| 0< x+y < \dfrac{\pi}{2} \bigg \} = 0.125 \text{ at } (x,y) \approx (0.523599, 0.523599)\\ \end{multline}\)
04/18/2021
Solve $\sqrt{x-\dfrac{1}{x}}+\sqrt{1-\dfrac{1}{x}}=x$
Solve:
$\sqrt{x-\dfrac{1}{x}}-\sqrt{1-\dfrac{1}{x}} = \dfrac{x-\dfrac{1}{x}-1+\dfrac{1}{x}}{\sqrt{x-\dfrac{1}{x}}+\sqrt{1-\dfrac{1}{x}}} = \dfrac{x-1}{x}$ $\implies 2\sqrt{x-\dfrac{1}{x}}=x-\dfrac{1}{x}+1$
Let $x-\dfrac{1}{x}=y \implies 2y=y^2+1 \implies y=1 \implies x-\dfrac{1}{x}=1$ $\implies x^2-x-1=0 \implies x=\dfrac{1\pm\sqrt{5}}{2}$
But $x \ge 0 \implies x=\bbox[1px, border: 1px solid black]{\dfrac{1+\sqrt{5}}{2}}$