December 2020

12/01/2020

For $n=1,2,3,… (\sqrt{2}-1)^n=\sqrt{m+1}-\sqrt{m}$ where $m$ is a positive integer which depends on $n$. Proof by (easy) mathematical induction. See American Mathematical Monthly, vol. 58, 1951, p. 566. Problem 15.53 From Mathematical Discovery by George Polya

Solution:

When $n=1$, $m_1=1$
When $n=2$, $(\sqrt{2}-1)^2=3-2\sqrt{2}=\sqrt{9}-\sqrt{8}, m_2=8$
Suppose $n=k$, $(\sqrt{2}-1)^k=\sqrt{m_k+1}-\sqrt{m_k}$, $m_k \in \mathbb{N}$, then

$(\sqrt{2}-1)^{k+1}=(\sqrt{m_k+1}-\sqrt{m_k})(\sqrt{2}-1)$ $=\sqrt{2m_k+2}+\sqrt{m_k}-\sqrt{m_k+1}-\sqrt{2m_k}$

Let $\sqrt{2m_k+2}+\sqrt{m_k}=\sqrt{m_{k+1}+1}$, then

$m_{k+1}=(\sqrt{2m_k+2}+\sqrt{m_k})^2-1$ $=3m_k+1+2\sqrt{2m_k^2+2m_k}$ $=(\sqrt{2m_k})^2+(\sqrt{m_k+1})^2+2\sqrt{2m_k(m_k+1)}$ $=(\sqrt{2m_k}+\sqrt{m_k+1})^2$ $\sqrt{m_{k+1}}=\sqrt{2m_k}+\sqrt{m_k+1}$ $\implies (\sqrt{2}-1)^{k+1}=\sqrt{m_{k+1}+1}-\sqrt{m_{k+1}}$ where $ m_{k+1}=3m_k+1+2 \sqrt{2m_k^2+2m_k} $

Now we need prove that $m_{k+1} \in \mathbb{N}$.

When $n=1$, $m_1=1$
When $n=2$, $m_2=3m_1+1+2\sqrt{2m_1^2+2m_1}=8$, and $\sqrt{2m_1^2+2m_1}=2 \in \mathbb{N}$
Suppose $n=k$, $m_k=3m_{k-1}+1+2\sqrt{2m_{k-1}^2+2m_{k-1}}$, and $\sqrt{2m_{k-1}^2+2m_{k-1}}=p \in \mathbb{N}$

So $m_k=3m_{k-1}+1+2p$, $p^2=2m_{k-1}^2+2m_{k-1}$

Then when $n=k+1$, $m_{k+1}=2m_k+1+2\sqrt{2m_k^2+2m_k}$, where

$2m_k^2+2m_k=2(3m_{k-1}+1+2p)(3m_{k-1}+2+2p)$

$=18m_{k-1}^2+18m_{k-1}+24pm_{k-1}+12p+4+8p^2$

$=34m_{k-1}^2+34m_{k-1}+24pm_{k-1}+12p+4$

$=(4m_{k-1}+3p+2)^2 \implies m_{k+1} \in \mathbb{N}$

The original statement has been proved. $\blacksquare$

12/01/2020

There are 10 stones in the pond as blue points in the figure. Frogs can jump from a stone to one of the adjacent stones only. Starting from a stone, how many different ways can a frog go for 4 jumps?

Solution 1:

Mark all stones with number 1 initially, then in each step, replace the number on each stone by the sum of numbers of its neighbors. Repeat this process for 4 steps as 4 jumps:

Initial: 3 corners: 1; 6 sides: 1; 1 center: 1
Step 1: 3 corners: 2; 6 sides: 4; 1 center: 6
Step 2: 3 corners: 8; 6 sides: 16; 1 center: 24
Step 3: 3 corners: 32; 6 sides: 64; 1 center: 96
Step 4: 3 corners: 128; 6 sides: 256; 1 center: 384

So the answer is $3 \times 128 + 6 \times 256 + 384=\bbox[1px, border: 1px solid black]{2304}$

Solution 2:

There are three types of stones in the figure: corner, side, center.

And there are 3 corners, 6 sides, 1 center. We mark this by a vector $\begin{equation*} \begin{bmatrix} 3 & 6 & 1 \end{bmatrix} \end{equation*} \text{.}$

Each number in the transfer matrix represents the number of ways of jump. The transfer matrix is designed as: $\begin{equation*} \begin{bmatrix} \text{<corner neighbors to corner>} & \text{<side neighbors to corner>} & \text{<center neighbors to corner>} \\ \text{<corner neighbors to side>} & \text{<side neighbors to side>} & \text{<center neighbors to side>} \\ \text{<corner neighbors to center>} & \text{<side neighbors to center>} & \text{<center neighbors to center>} \end{bmatrix} \end{equation*}$

So the transfer matrix $A$ is: $\begin{equation*} A= \begin{bmatrix} 0 & 2 & 0 \\ 1 & 2 & 1 \\ 0 & 6 & 0 \end{bmatrix} \end{equation*} \text{.}$

The number of different ways for a frog can go for $n$ jumps is: $\begin{equation*} \begin{bmatrix} 3 & 6 & 1 \end{bmatrix} A^n \end{equation*} \text{.}$

This will get a vector of dimension $1 \times 3$ for three types, and we need sum them up by multipling vector $\begin{equation*} \begin{bmatrix} 1\\ 1\\ 1 \end{bmatrix} \end{equation*} \text{.}$ So the expression is $\begin{equation*} \begin{bmatrix} 3 & 6 & 1 \end{bmatrix} A^n \begin{bmatrix} 1\\ 1\\ 1 \end{bmatrix} \end{equation*} \text{.}$ When $n=4$, the answer is $\begin{equation*} \begin{bmatrix} 3 & 6 & 1 \end{bmatrix} A^4 \begin{bmatrix} 1\\ 1\\ 1 \end{bmatrix} \end{equation*} =\bbox[1px, border: 1px solid black]{2304} \text{.}$

The calculation is given here.

12/02/2020

A 4-digit number divides each of its 4 digits will get 4 integers. And the sum of these 4 digits equals to the 4-digit number itself. How many numbers satisfy this requirement?

Solution:

Apparently there is no zero and one in digits.

12/02/2020

If $a,b \in \mathbb{N}$ such that $\dfrac{2019}{2020}<\dfrac{a}{b} < \dfrac{2020}{2021}$, what is the smallest possible value of $a+b?$

Solution:

$\dfrac{2019}{2020}<\dfrac{a}{b} < \dfrac{2020}{2021}$

$\implies a<b \implies b \ge a + 1 \implies b-a \ge 1$ and

$\implies \dfrac{2020}{2019} > \dfrac{b}{a} > \dfrac{2021}{2020}$

$\implies \dfrac{1}{2019} > \dfrac{b-a}{a} > \dfrac{1}{2020}$

$\implies 2019 < \dfrac{a}{b-a} < 2020$

When $(b-a)_{min} = 1$, $2019 < a < 2020 \implies a \not\in \mathbb{N} $

When $(b-a)_{min} = 2$, $4038 < a < 4040 \implies a=4039$

$\implies b=a+2=4041 \implies (a+b)_{min}=\bbox[1px, border: 1px solid black]{8080}$

12/02/2020

If $\dfrac{1}{6}=\dfrac{1}{a_1}+\dfrac{1}{a_2}+\dfrac{1}{a_3}+\dfrac{1}{a_4}+\dfrac{1}{a_5}+\dfrac{1}{a_6}$ and $a_i \in \mathbb{N}$, $\forall i \ne j, a_i \ne a_j$. What is the smallest possible value of $\displaystyle \sum_{i=1}^{6}a_i.$

Solution:

12-03-2020

Solve for real values of $x$: $2\sqrt[3]{2x+1}=x^3-1$

Solution:

Let $y=\sqrt[3]{2x+1} \implies x=\dfrac{y^3-1}{2}$

$\implies 2y=x^3-1 \implies y=\dfrac{x^3-1}{2}$

Let $f(w)=\dfrac{w^3-1}{2}$, $f(w)$ is a restrictly increasing function, $x=f(y)$, $y=f(x)$.

Assume $x<y$, since $f(w)$ is restrictly increasing, $f(x)<f(y) \implies y < x$

Similarly assume $x>y$ will get contradictory result, so we have $x=y$

$x=\dfrac{x^3-1}{2} \implies (x^2-x-1)(x+1)=0$

$x=\bbox[1px, border: 1px solid black]{-1, \dfrac{1\pm \sqrt{5}}{2}}$

12/03/2020

For what $x \in \mathbb{N}$ are $8x^3-20$ and $2x^5-2$ both perfect squares $?$

Solution:

Let $8x^3-20=m^2$, $2x^5-2=n^2$, for $m,n \in \mathbb{N}$

Then $m^2 \cdot n^2=(8x^3-20)(2x^5-2)=16x^8-40x^5-16x^3+40=(mn)^2$

$16x^8-40x^5-16x^3+40=(4x^4-5x)^2-(16x^3+25x^2-40)$

$=(4x^4-5x-1)^2+(8x^4-16x^3-25x^2-10x+39)$

Let $f(x)=16x^3+25x^2-40$, $g(x)=8x^4-16x^3-25x^2-10x+39$

When $x\ge 4$, $f(4)>0, f’(4)>0 \implies (mn)^2<(4x^4-5x)^2$

$g(x)>8x^4-16x^3-32x^2-16x+39$, Let $h(x)=8x^4-16x^3-32x^2-16x+39$

When $x\ge 4$, $h(4)>0, f’(4)>0 \implies (mn)^2>(4x^4-5x-1)^2$

This is contraductory, so we know $x<4, x \in \mathbb{N}$

When $x=1, m^2=-16 < 0$, not a solution

When $x=2, m^2=44$, not a solution

When $x=3, m^2=196 \implies m=13, n^2=484 \implies n=22$

So the solution is $x=\bbox[1px, border: 1px solid black]{3}$

12/04/2020

Tessa has a unit cube, on which each vertex is labeled by a distinct integer between 1 and 8 inclusive. She also has a deck of 8 cards, 4 of which are black and 4 of which are white. At each step she draws a card from the deck, and

if the card is black, she simultaneously replaces the number of each vertex by the sum of the three numbers on vertices that are distance 1 away from this vertex;
if the card is white, she simultaneously replaces the number of each vertex by the sum of the three numbers on vertices that are distance $\sqrt{2}$ away from this vertex.

When Tessa finishes drawing all cards of the deck, what is the maximum possible value of a number that is on the cube?

Solution:

12/04/2020

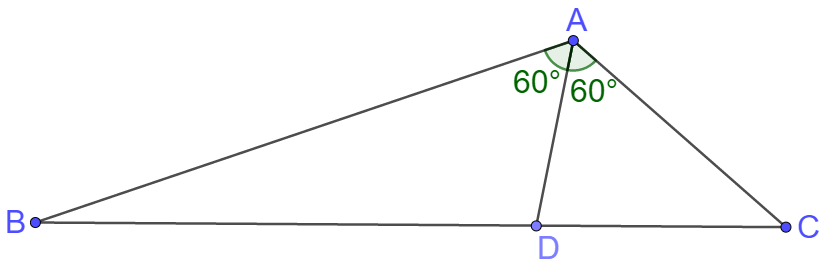
$\angle{BAD}=\angle{DAC}=60^{\circ}, \dfrac{AB}{AC}=2, AD=100$, solve $BC.$

Solution:

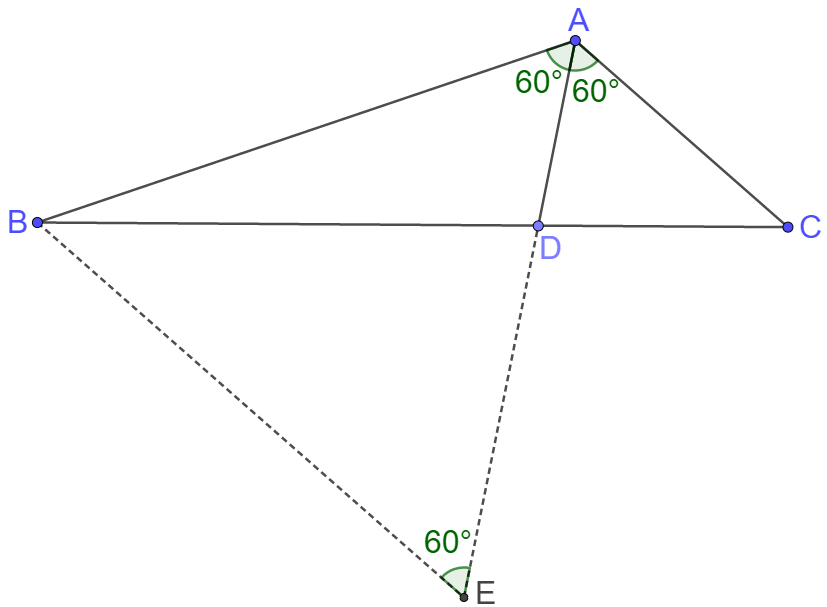
$AD$ bisects $\angle{BAC} \implies \dfrac{AB}{AC}=\dfrac{BD}{CD}=2$

Extend $AD$ to $E$ so that $\angle{AEB}=60^{\circ}$. Easy to know $\triangle{ABE}$ is equilateral and $\triangle{DBE} \sim \triangle{DAC}$

$\implies \dfrac{DE}{AD}=\dfrac{BE}{AC}=\dfrac{BD}{CD}=2$

$\implies DE=200 \implies AB=BE=AE=300 \implies AC=150$

$\implies BC^2=AB^2+AC^2-2AB \cdot AC \cdot cos\angle{BAC}$

$\implies BC^2=300^2+150^2+2\times 300 \times 150 \times \dfrac{1}{2}$

$ \implies BC=\bbox[1px, border: 1px solid black]{150\sqrt{7}}$

12/04/2020

Points $O$ and $H$ are the circumcentre and orthocentre of acute triangle $ABC$, respectively. The perpendicular bisector of segment $AH$ meets sides $AB$ and $AC$ at $D$ and $E$, respectively. Prove that $\angle{DOA}=\angle{EOA}.$

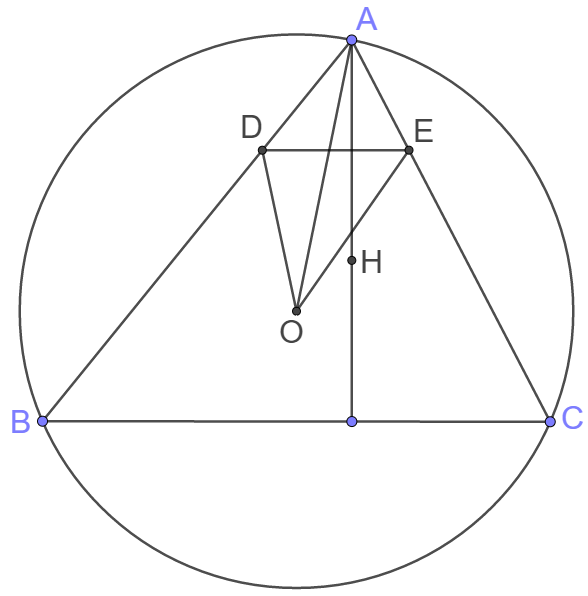
Proof:

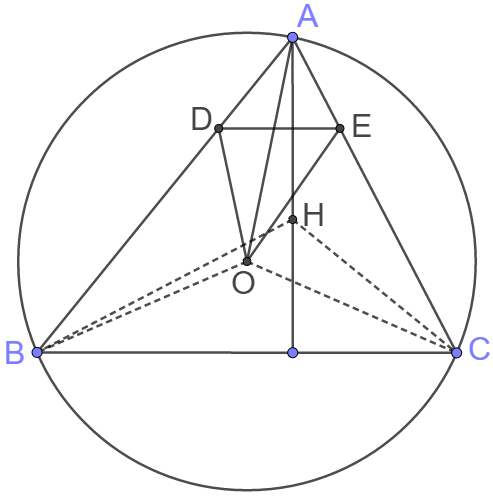
Since points $O$ and $H$ are the circumcentre and orthocentre of acute triangle $ABC$, they are isogonal conjugates.

That means, $\angle{BAO} = \angle{HAC} \implies \angle{BAH} = \angle{OAC}$

$AD=DH, AO=OC, \angle{BAH} = \angle{OAC} \implies \triangle{DAH} \sim \triangle{OAC}$

$\implies \dfrac{AD}{AH}=\dfrac{AO}{AC}$, and we know $\angle{BAO} = \angle{HAC}$

$\implies \triangle{ADO} \sim \triangle{AHC} \implies \angle{DOA}=\angle{HCA}$

$\implies \angle{HCA}=\angle{OCB}=\angle{OBC}=\angle{ABH}$

Similarly, $\triangle{AEO} \sim \triangle{AHB} \implies \angle{AOE}=\angle{ABH}$

So we know $\angle{DOA}=\angle{AOE} \blacksquare$

12/04/2020

Given $a_1,a_2,…,a_n \in \mathbb{N}, n>4$, prove: there exist $x_1,x_2,…,x_n \in \mathbb{R}$ such that $\displaystyle\prod_{i=1}^{n}{x_i} \ne 0$, $x_2=0$ or $1$, satisfying $\displaystyle\sum_{i=1}^{n}{a_ix_i} \equiv 0$ mod $n^2.$

Solution:

12/05/2020

In a barn, 100 chicks sit peacefully in a circle. Suddenly, each chick randomly pecks the chick immediately to its left or right with equal chance. What is the expected number of unpecked chicks$?$

Solution:

Let $\begin{align*} X_i= \begin{cases} \text{ 0 if the chick is pecked}\\ \text{ 1 if the chick is unpecked} \end{cases} \end{align*}\\$

Let $P_r(\text{check pecks left})=p$ and $P_r(\text{chick pecks right})=1-p$ $\begin{align*} E(X_i) &= 0 \times Pr(\text{pecked}) + 1 \times Pr(\text{unpecked})\\ &= P_r(\text{unpecked})\\ &=Pr(\text{chick on left pecks left}) \times P_r(\text{chick on right pecks right})\\ &=p(1-p) \end{align*}\\$

Based on Linearity of expectation $E(X+Y)=E(X)+E(Y)$: $\begin{align*} E(X_1+X_2+...+X_{100})&=E(X_1)+E(X_2)+...+E(X_{100})\\ &=p(1-p)+p(1-p)+...+p(1-p)\\ &=100p(1-p)\\ \end{align*}$

When $p=0.5$, the answer is $\bbox[1px, border: 1px solid black]{25}$.

12/06/2020

Let $a$ be the greatest root of $x^3-3x^2+1=0$. Show $\lfloor {a^{1988}} \rfloor$ is divisible by $17.$

Solution:

12/08/2020

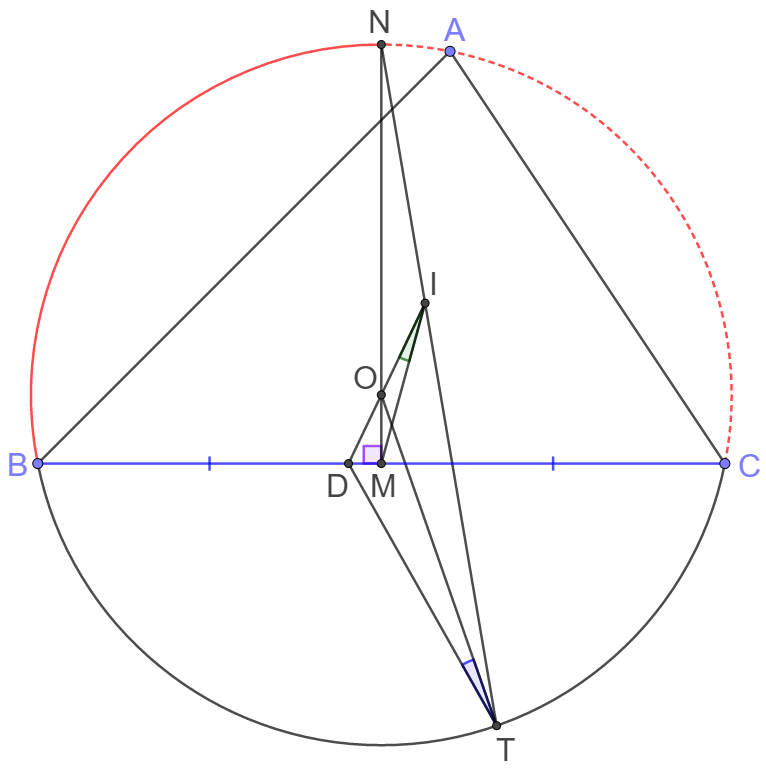
Point $O$ and $I$ is circumcenter and incenter of $\triangle{ABC}$ respectively. Point $N$ bisects $\overset{\huge\frown}{BC}$ and point $M$ bisects segment $BC$. Extend $NI$ and intersect circle $O$ at point $T$. Extend $IO$ and intersect $BC$ at point $D$. Prove: $\angle{DTO}=\angle{DIM}.$

12/10/2020

Let $A, B, C, D$ be points chosen on a circle, in that order. Line $BD$ is reflected over lines $AB$ and $DA$ to obtain lines $l_1$ and $l_2$ respectively. If lines $l_1, l_2$ and $AC$ meet at a common point and if $AB=4$, $BC=3$, $CD=2$, compute the length $DA.$

Solution:

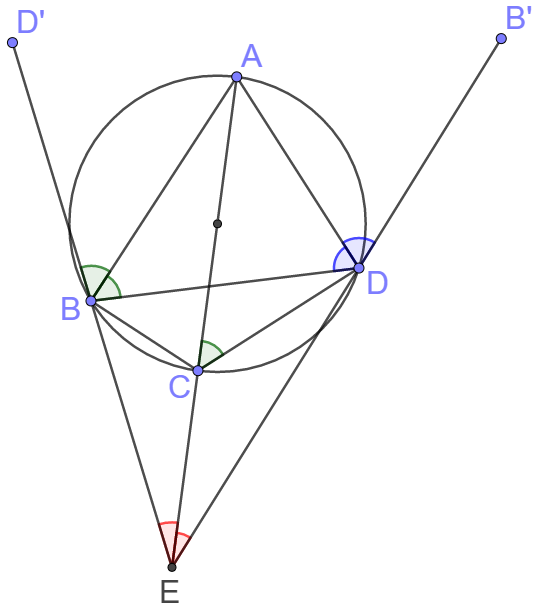
Line $BD$ is reflected over lines $AB$ and $DA$ to obtain line $BD’$ and $DB’$, then we know $AB$ bisects $\angle{DBD’}$ and $AD$ bisects $\angle{BDB’}$. That means point $A$ is an excenter of $\triangle{BDE}$, then we know $AE$ bisects $\angle{BED}$ and since point $C$ is on line $AE$ and also on the excircle ${ABCD}$, $C$ is the incenter of $\triangle{BDE}$, and $AC$ is actually the diameter of the excircle. That is,

$AC^2=AB^2+BC^2=CD^2+AD^2$

$ \implies AD=\sqrt{AB^2+BC^2-CD^2}=\bbox[1px, border: 1px solid black]{\sqrt{21}}$

To prove $C$ is the incenter of $\triangle{BDE}$ and $AC$ is the diameter of the excircle $ABCD$ of $\triangle{BDE}$, there are two references:

First, by the trigonometric form of Ceva’s theorem, the internal angle bisector of $\angle{BED}$ must be concurrent with the external angle bisectors of $\angle{DBE}$ and $\angle{BDE}$. Thus we know AE bisects $\angle{BED}$.

Second, by angle chasing, we know

$\angle{D’BA}=\angle{ABD}=\angle{BEA}+\angle{BAE}$

$\angle{B’DA}=\angle{ADB}=\angle{AED}+\angle{EAD}$

Add above two we get

$180^{\circ}-\angle{BAD}=2\angle{BEA}+\angle{BAD}$

$\implies \angle{BEA}+\angle{BAD}=90^{\circ}$

$\angle{BEA}+\angle{BAE}+\angle{EAD}=90^{\circ}$

$\implies \angle{D’BA}=\angle{ABD}=\angle{ACD}=90^{\circ}-\angle{CAD}$

$\implies \angle{ADC}=\angle{ADB}+\angle{BDC}=90^{\circ}=\dfrac{2\angle{ADB}+\angle{BDE}}{2}=\angle{ADB}+\dfrac{\angle{BDE}}{2}$

$\implies \angle{BDC}=\dfrac{\angle{BDE}}{2}$

And similarly $\angle{DBC}=\dfrac{\angle{DBE}}{2}$, so $C$ is the incenter of $\triangle{BDE}$ and $AC$ is the diameter of circle $ABCD\blacksquare$.

12/17/2020

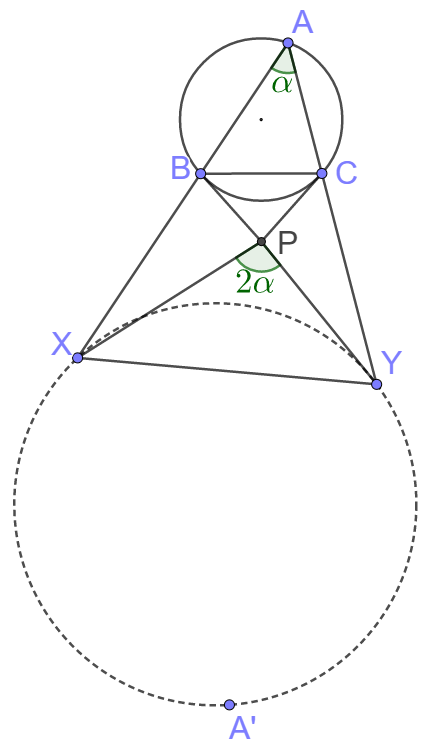
Tangents of the circumcircle of Acute $\triangle{ABC}$ at point $B$ and $C$ intersect at point $P$. Point $X$ and $Y$ are on extension of line $AB$ and $AC$ respectively, and $\angle{XPY}=2\angle{A}$. Reflect $A$ about line $XY$ and get $A’$. Prove: the circumcircle of $\triangle{A’XY}$ passes through a fixed point.

12/20/2020

Let $a$, $b$ and $c$ be positive integers with $a \ge b \ge c$ such that

$\begin{align} a^2-b^2-c^2+ab &= 2011 \tag{1}\\ a^2+3b^2+3c^2-3ab-2ac-3bc &= -1997 \tag{2} \end{align}$

What is $a?$ (AMC 10 2011-A Problem 24)

Solution:

$(1) + (2) \implies$ $ a^2+b^2+c^2-ab-bc-ca=7 $ $\implies (a-b)^2+(b-c)^2+(c-a)^2=14 $

Since $a$, $b$ and $c$ be positive integers with $a \ge b \ge c$

$\implies a-c=3, a-b=1, b-c=2$ or $a-c=3, a-b=2, b-c=1$

if $a-b=2$, $(1) \implies 7a=2021$, no solution
if $a-b=1$, $(1) \implies 8a=2024 \implies a=\bbox[1px, border: 1px solid black]{253}$

12/20/2020

The sum of the first $m$ positive odd integers is 212 more than the sum of the first $n$ positive even integers. What is the sum of all possible values of $n?$ (AMC 10 2011-A Problem 24)

Solution:

The sum of the first $m$ positive odd integers is $1+3+…+(2m-1)=m+0+2+…+(2m-2)=m+m(m-1)=m^2$.

The sum of the first $n$ positive even integers is $2+4+…+2n=n(n+1)$.

So we have $n^2+n+212-m^2=0$, the discriminant is $1-4(212-m^2)=4m^2-847$ must be a square of an odd integer. Let $p^2=4m^2-847 \implies (2m+p)(2m-p)=847$. $847=71111$, so we know there could be three situations:

$2m+p=847, 2m-p=1 \implies m=212, p=423 \implies n=211$
$2m+p=121, 2m-p=7 \implies m=32, p=57 \implies n=28$
$2m+p=77, 2m-p=11 \implies m=22, p=33 \implies n=16$

So the sum of all possible values of $n$ is $\bbox[1px, border: 1px solid black]{255}$.

12/20/2020

Adam, Benin, Chiang, Deshawn, Esther, and Fiona have internet accounts. Some, but not all, of them are internet friends with each other, and none of them has an internet friend outside this group. Each of them has the same number of internet friends. In how many different ways can this happen? (AMC 10 2012-A Problem 23)

Solution:

Each has 1 internet friend: $5*3=15$ (Three lines: for A, choose 1 from 5 to make a pair, then one of the rest person choose 1 from 3 to make a pair, the rest 2 makes a pair)
Each has 2 internet friends: $\binom{5}{2} + \binom{5}{2} \times \binom{3}{1} \times \binom{2}{1}=70$ (a hexagon or two small triangles)
Each has 3 internet friends: $\binom{5}{3} + \binom{5}{3} \times \binom{3}{2} \times \binom{2}{1}=70$ (for A, choose 3 from 5 to make friends, then left 2 persons not friend of A. Consider one of the two, he can share 3 friends with A, then the last person also shares three friends with A; or he can share 2 friends out of 3 with A, then make friend with the last person, now there are 2 people with 2 friends, 2 people with 2 friend, th former choose 1 of the latters, then the rest connections are determined; or he can share 1 friends out of 3 with A)
Each has 4 internet friends: $\binom{5}{4} \times \binom{3}{2} = 15$ (for A, choose 4 from 5 to make friends, then there is the last person not being A’s friends, and must have all A’s friends as his/her friends. Then one of their common 4 friends chooses 2 from the other three as his/her friends, the last of the common friend has no other choice than share these two friends)

So there are totally $15+70+70+15=\bbox[1px, border: 1px solid black]{170}$ different ways.

12/20/2020

$ABCD$ is a trapezoid. $AD \parallel BC, S_{\triangle{ACE}}=S_{\triangle{BDE}}=120, S_{\triangle{BFG}}=60$. What is the area of $ABCD?$

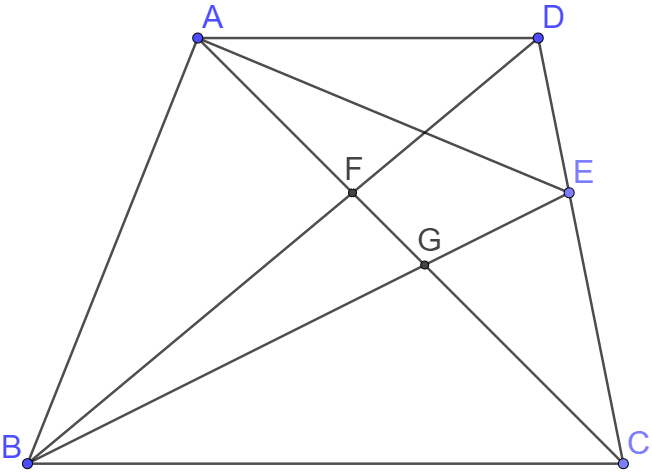
Solution:

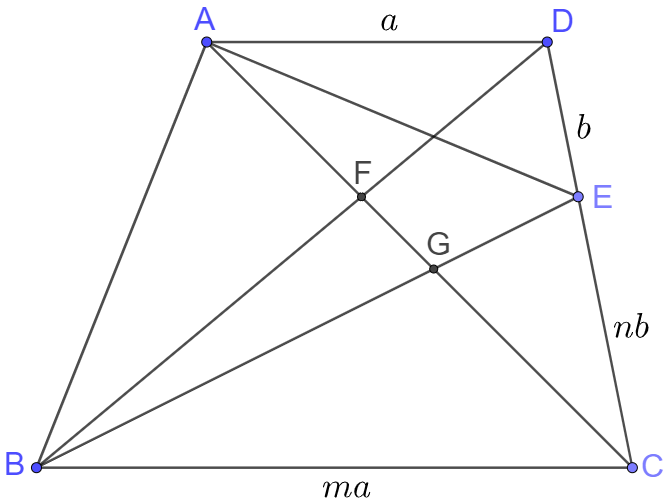\(\begin{multline}\nonumber \shoveleft \text{Suppose } AD=a, BC=m\cdot AD = ma, DE=b, CE=n \cdot DE = nb \\ \shoveleft \implies \dfrac{BC}{AD}=\dfrac{CF}{AF}=\dfrac{BF}{DF}=m, [BCF]=m^2[ADF] \implies \dfrac{FB}{BD}=\dfrac{m}{m+1}\\ \shoveleft \implies \dfrac{[BCD]}{[ACD]}=m \implies \dfrac{[BCE]+[BDE]}{[ADE]+[ACE]}=m\\ \shoveleft \implies \dfrac{(1+n)[BDE]}{(1+\cfrac{1}{n})[ACE]}=m, [ACE]=[BDE] \implies m=n\\ \shoveleft \text{Apply Menelaus's theorem to } \triangle{CDF} \text{ and line } BE \implies \dfrac{DE}{EC}\dfrac{CG}{GF}\dfrac{FB}{BD}=1 \\ \shoveleft \implies \dfrac{1}{n}\dfrac{CG}{GF}\dfrac{m}{m+1}=1 \implies \dfrac{CG}{GF}=\dfrac{(m+1)n}{m} \implies [BCG]=(m+1)[BFG]\\ \shoveleft \implies [BCF]=[BCG]+[BFG]=(m+2)[BFG]\\ \shoveleft \implies [ADF]=\dfrac{1}{m^2}[BCF]=\dfrac{m+2}{m^2}[BFG], [ABF]=[CDF]=\dfrac{1}{m}[BCF]=\dfrac{m+2}{m}[BFG]\\ \shoveleft \implies [ACD]=[ADF]+[CDF]=[ADE]+[ACE] \implies \dfrac{m+2}{m^2}[BFG]+\dfrac{m+2}{m}[BFG]=\dfrac{m+1}{m}[ACE]\\ \shoveleft \implies \dfrac{m+2}{m^2}\cdot 60 + \dfrac{m+2}{m} \cdot 60 = \dfrac{m+1}{m} \cdot 120 \implies m^2-m-2=0 \implies m=2\\ \shoveleft [ABCD]=[ABF]+[BCF]+[ACD]=2\cdot [BFG]+4 \cdot[BFG]+\dfrac{3}{2} \cdot [ACE]=6 \cdot 60 + \dfrac{3}{2} \cdot 120=\bbox[5px, border: 1px solid black]{540}\\ \end{multline}\)

12/21/2020

A $3 \times 3$ square is partitioned into 9 unit squares. Each unit square is painted either white or black with each color being equally likely, chosen independently and at random. The square is then rotated $90^{\circ}$ clockwise about its center, and every white square in a position formerly occupied by a black square is painted black. The colors of all other squares are left unchanged. What is the probability that the grid is now entirely black? (AMC 10 2012-A Problem 20)

Solution:

The center square has $\dfrac{1}{2}$ chance to be black.
The 4 corners will be all black if they are BBBB, BBBW, BWBW, WBWB, BBWB, BWBB, WBBB, so it’s $\dfrac{7}{16}$ chance to be all black.
Similarly the 4 squares not on corner nor in center will be all black if they are BBBB, BBBW, BWBW, WBWB, BBWB, BWBB, WBBB, and it’s also $\dfrac{7}{16}$ chance to be all black.

Thus totally the probability that the grid is entirely black: $\dfrac{1}{2} \times \dfrac{7}{16} \times \dfrac{7}{16} = \bbox[1px, border: 1px solid black]{\dfrac{49}{512}}$

12/21/20202

Real numbers $x$, $y$, and $z$ are chosen independently and at random from the interval $[0, n]$ for some positive integer $n$. The probability that no two of $x$, $y$, and $z$ are within 1 unit of each other is greater than $\dfrac{1}{2}$. What is the smallest possible value of $n?$

Solution:

12/22/2020

In a round-robin tournament with 6 teams, each team plays one game against each other team, and each game results in one team winning and one team losing. At the end of the tournament, the teams are ranked by the number of games won. What is the maximum number of teams that could be tied for the most wins at the end of the tournament? (AMC 10 2012-B Problem 15)

Solution:

There are $\binom{6}{2} = 15$ games played, so it’s impossible for 6 teams to win equal number of games. It is possible for 5 teams to win equally. 5 teams each wins 3 games and the rest team wins 0 games.

12/23/2020

Suppose that one of every $500$ people in a certain population has a particular disease, which displays no symptoms. A blood test is available for screening for this disease. For a person who has this disease, the test always turns out positive. For a person who does not have the disease, however, there is a $2%$ false positive rate—in other words, for such people, $98%$ of the time the test will turn out negative, but $2%$ of the time the test will turn out positive and will incorrectly indicate that the person has the disease. Let $p$ be the probability that a person who is chosen at random from this population and gets a positive test result actually has the disease. Which of the following is closest to $p?$ (AMC 10 2011-B Problem 18)

$(A) \dfrac{1}{98} \hspace{5mm} (B) \dfrac{1}{9} \hspace{5mm} (C) \dfrac{1}{11} \hspace{5mm} (D) \dfrac{49}{99} \hspace{5mm} (E) \dfrac{98}{99}$

Solution:

This problem is a reading problem at first. What is asked to solve? Choose a person at random and what is probability he actually has the disease? No. For second think, it’s asking when a person is chosen at random from this population and gets a positive test result, what is the probability he actually has the disease.

How many people will get positive test result from $500$ people? $1 + 0.02 \times 499$

How many of them actually has the disease: $1$

So the answer is $\dfrac{1}{1+\dfrac{499}{50}} \approx \dfrac{50}{550} = \bbox[1px, border: 1px solid black]{\dfrac{1}{11}}$

12/23/2020

Jesse cuts a circular paper disk of radius $12$ along two radii to form two sectors, the smaller having a central angle of $120$ degrees. He makes two circular cones, using each sector to form the lateral surface of a cone. What is the ratio of the volume of the smaller cone to that of the larger? (AMC 10 2011-B Problem 17)

Solution:

12/29/2020

Prove that when $p>3$ is a prime, $p!+p$ cannot be a perfect square.

12/31/2020

New Year Problem: Find $r$ in following diagram:

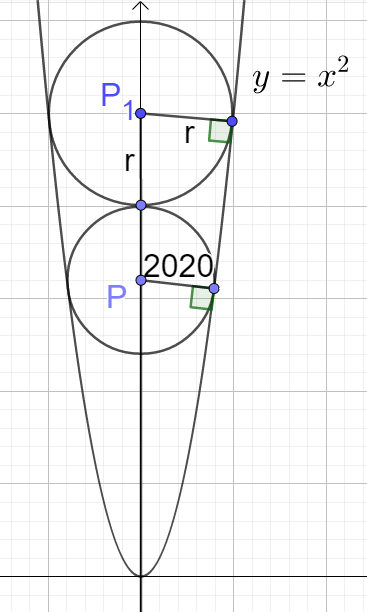
Solution:

Let’s use $r$ and $r_1$ to work on general result and then replace $r=2020$ to get the answer.

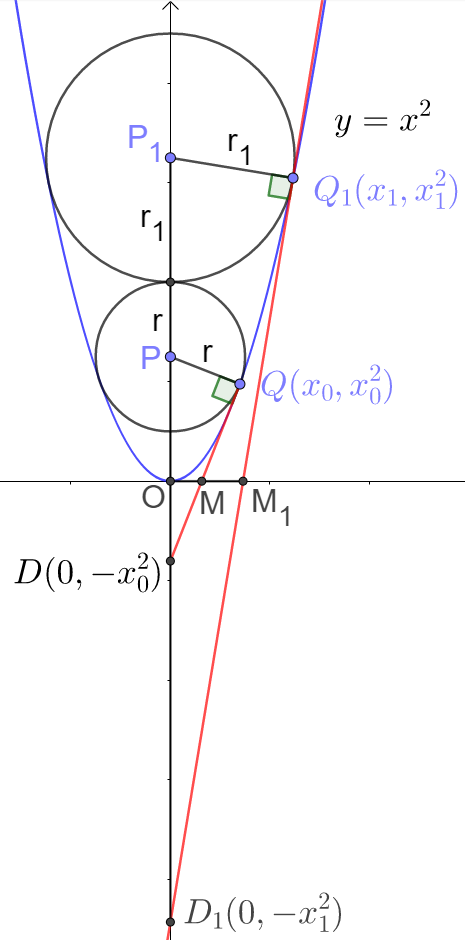
Suppose the tangent line at point $Q(x_0, x_0^2)$ is $y=2x_0x+d_0$, then

$x_0^2=2x_0^2+d_0 \implies d_0=-x_0^2 \implies y=2x_0x-x_0^2$

So we get $D(0, -x_0^2) \implies OD=x_0^2, OM=\dfrac{x_0}{2}, QD^2=x_0^2+4x_0^4$

$\dfrac{OD}{OM}=\dfrac{PD}{PQ} \implies QD=\dfrac{rx_0^2}{x_0/2}=2rX_0$

$QD^2=x_0^2+4x_0^4=4r^2 \cdot x_0^2 \implies x_0^2=\dfrac{4r^2-1}{4}$

$PD^2=QD^2+PQ^2=4r^2 \cdot \dfrac{4r^2-1}{4}+r^2 $

$\implies PD=\dfrac{4r^2}{2}=2r^2$

Similarly, suppose the tangent line at $Q_1(x_1,x_1^2)$ is $y=2x_1x+d_1$, then

$y=2x_1x-x_1^2$, $x_1^2=\dfrac{4r_1^2-1}{4}$, $Q_1D_1^2=4r_1^4-r^2$, $P_1D_1=2r_1^2$

$P_1D_1=PD+r+r_1+(x_1^2-x_0^2)=2r_1^2$

$\implies 2r_1^2 = 2r^2 + r + r_1 + \dfrac{4r_1^2-1}{4} - \dfrac{4r^2-1}{4}$

$\implies r_1^2-r_1=r^2+r \implies r_1(r_1-1)=r(r+1)$

$\implies r_1=r+1$

$r=2020 \implies r_1=\boxed{2021}$

PREVIOUSNovember 2020

NEXTJanuary 2021

12/01/2020

For $n=1,2,3,… (\sqrt{2}-1)^n=\sqrt{m+1}-\sqrt{m}$ where $m$ is a positive integer which depends on $n$. Proof by (easy) mathematical induction. See American Mathematical Monthly, vol. 58, 1951, p. 566. Problem 15.53 From Mathematical Discovery by George Polya

12/01/2020

There are 10 stones in the pond as blue points in the figure. Frogs can jump from a stone to one of the adjacent stones only. Starting from a stone, how many different ways can a frog go for 4 jumps?

12/02/2020

A 4-digit number divides each of its 4 digits will get 4 integers. And the sum of these 4 digits equals to the 4-digit number itself. How many numbers satisfy this requirement?

12/02/2020

If $a,b \in \mathbb{N}$ such that $\dfrac{2019}{2020}<\dfrac{a}{b} < \dfrac{2020}{2021}$, what is the smallest possible value of $a+b?$

12/02/2020

If $\dfrac{1}{6}=\dfrac{1}{a_1}+\dfrac{1}{a_2}+\dfrac{1}{a_3}+\dfrac{1}{a_4}+\dfrac{1}{a_5}+\dfrac{1}{a_6}$ and $a_i \in \mathbb{N}$, $\forall i \ne j, a_i \ne a_j$. What is the smallest possible value of $\displaystyle \sum_{i=1}^{6}a_i.$

12-03-2020

Solve for real values of $x$: $2\sqrt[3]{2x+1}=x^3-1$

12/03/2020

For what $x \in \mathbb{N}$ are $8x^3-20$ and $2x^5-2$ both perfect squares $?$

12/04/2020

Tessa has a unit cube, on which each vertex is labeled by a distinct integer between 1 and 8 inclusive. She also has a deck of 8 cards, 4 of which are black and 4 of which are white. At each step she draws a card from the deck, and

if the card is black, she simultaneously replaces the number of each vertex by the sum of the three numbers on vertices that are distance 1 away from this vertex;

if the card is white, she simultaneously replaces the number of each vertex by the sum of the three numbers on vertices that are distance $\sqrt{2}$ away from this vertex.

When Tessa finishes drawing all cards of the deck, what is the maximum possible value of a number that is on the cube?

12/04/2020

$\angle{BAD}=\angle{DAC}=60^{\circ}, \dfrac{AB}{AC}=2, AD=100$, solve $BC.$

12/04/2020

Points $O$ and $H$ are the circumcentre and orthocentre of acute triangle $ABC$, respectively. The perpendicular bisector of segment $AH$ meets sides $AB$ and $AC$ at $D$ and $E$, respectively. Prove that $\angle{DOA}=\angle{EOA}.$

12/04/2020

Given $a_1,a_2,…,a_n \in \mathbb{N}, n>4$, prove: there exist $x_1,x_2,…,x_n \in \mathbb{R}$ such that $\displaystyle\prod_{i=1}^{n}{x_i} \ne 0$, $x_2=0$ or $1$, satisfying $\displaystyle\sum_{i=1}^{n}{a_ix_i} \equiv 0$ mod $n^2.$

12/05/2020

In a barn, 100 chicks sit peacefully in a circle. Suddenly, each chick randomly pecks the chick immediately to its left or right with equal chance. What is the expected number of unpecked chicks$?$

12/06/2020

Let $a$ be the greatest root of $x^3-3x^2+1=0$. Show $\lfloor {a^{1988}} \rfloor$ is divisible by $17.$

12/08/2020

Point $O$ and $I$ is circumcenter and incenter of $\triangle{ABC}$ respectively. Point $N$ bisects $\overset{\huge\frown}{BC}$ and point $M$ bisects segment $BC$. Extend $NI$ and intersect circle $O$ at point $T$. Extend $IO$ and intersect $BC$ at point $D$. Prove: $\angle{DTO}=\angle{DIM}.$

12/10/2020

Let $A, B, C, D$ be points chosen on a circle, in that order. Line $BD$ is reflected over lines $AB$ and $DA$ to obtain lines $l_1$ and $l_2$ respectively. If lines $l_1, l_2$ and $AC$ meet at a common point and if $AB=4$, $BC=3$, $CD=2$, compute the length $DA.$

12/17/2020

12/20/2020

Let $a$, $b$ and $c$ be positive integers with $a \ge b \ge c$ such that

What is $a?$ (AMC 10 2011-A Problem 24)

12/20/2020

The sum of the first $m$ positive odd integers is 212 more than the sum of the first $n$ positive even integers. What is the sum of all possible values of $n?$ (AMC 10 2011-A Problem 24)

12/20/2020

12/20/2020

$ABCD$ is a trapezoid. $AD \parallel BC, S_{\triangle{ACE}}=S_{\triangle{BDE}}=120, S_{\triangle{BFG}}=60$. What is the area of $ABCD?$

12/21/2020

12/21/20202

Real numbers $x$, $y$, and $z$ are chosen independently and at random from the interval $[0, n]$ for some positive integer $n$. The probability that no two of $x$, $y$, and $z$ are within 1 unit of each other is greater than $\dfrac{1}{2}$. What is the smallest possible value of $n?$

12/22/2020

12/23/2020

12/23/2020

12/29/2020

Prove that when $p>3$ is a prime, $p!+p$ cannot be a perfect square.

12/31/2020

New Year Problem: Find $r$ in following diagram: