11/05/2020
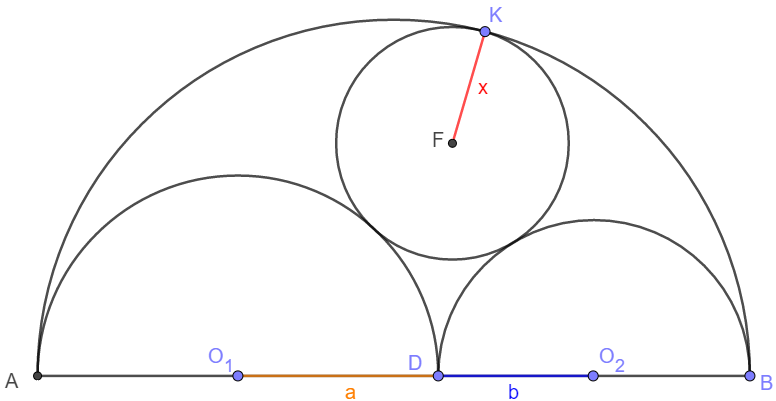
Prove $\dfrac{1}{x}=\dfrac{1}{a} + \dfrac{1}{b}-\dfrac{1}{a+b}$
Proof:
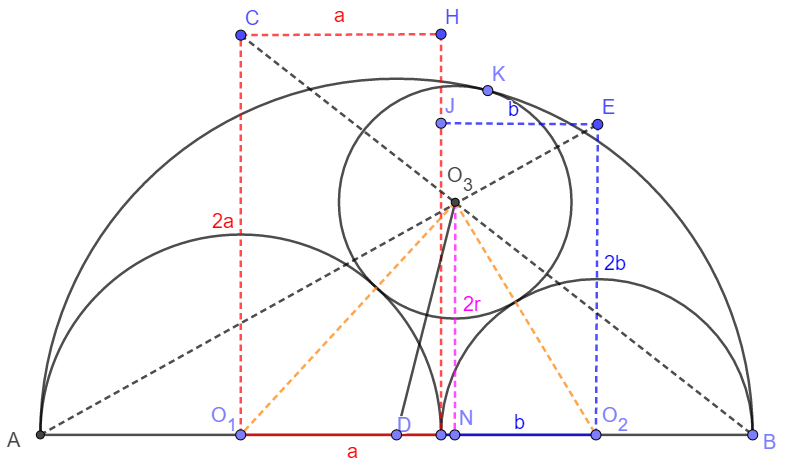
Take the three centers of the circles:
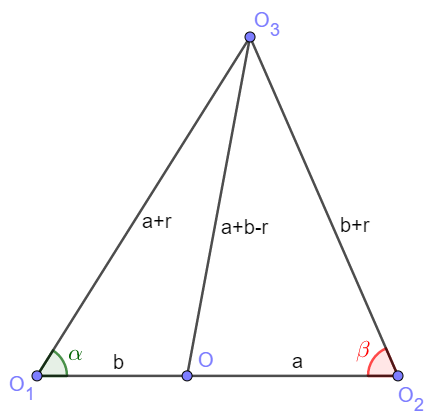
From the Law of Cosines:
$cos \alpha = \dfrac{(a+r)^2+b^2-(a+b-r)^2}{2b(a+r)}=\dfrac{1ar+br-ab}{b(a+r)}$
$cos \beta=\dfrac{(b+r)^2=a^2-(a+b-r)^2}{2a(b+r)}=\dfrac{2br+ar-ab}{a(b+r)}$
From the Law of Sines:
$\dfrac{b+r}{sin \alpha}=\dfrac{a+r}{sin \beta} \implies (a+r)^2(1-cos^2 \alpha)=(b+r)^2(1-cos^2 \beta)$
$\implies (a+r)^2-\dfrac{(2ar+br-ab)^2}{b^2}=(b+r)^2-\dfrac{(2br+ar-ab)}{a^2}$
$\implies (a+r)^2-(b+r)^2=\dfrac{a^2(2ar+br-ab)^2-b^2(2br+ar-ab)^2}{a^2b^2}$
$\implies a^2b^2(a+b+2r)(a-b)=(2a^2r+abr-a^2b+2b^2r+abr-ab^2)(2a^2r+abr-a^2b-2b^2r-abr+ab^2)$
$\implies a^2b^2(a+b+2r)(a-b)=[2(a^2+b^2+ab)r-ab(a+b)][2r(a+b)(a-b)-ab(a-b)]$
$\implies a^2b^2(a+b+2r)=[2(a^2+b^2+ab)r-ab(a+b)][2(a+b)r-ab]$
$\implies 2a^2b^2r+a^2b^2(a+b)=4(a+b)(a^2+b^2+ab)r^2-[2ab(a^2+b^2+ab)+2ab(a+b)^2]r+a^2b^2(a+b)$
$\implies a^2b^2=2(a+b)(a^2+b^2+ab)r-ab(2a^2+2b^2+3ab)$
$\implies (a+b)(a^2+b^2+ab)r=ab(a+b)^2 \implies r=\dfrac{ab(a+b)}{a^2+b^2+ab}$
$\implies r=\dfrac{ab(a+b)}{a^2+b^2+ab} \implies \dfrac{a+b}{r}=\dfrac{a^2+b^2+ab}{ab}$
$\implies \dfrac{a+b}{r}=\dfrac{(a+b)^2}{ab}-1 \implies \dfrac{1}{r}=\dfrac{a+b}{ab}-\dfrac{1}{a+b}$
$\implies \dfrac{1}{r}=\dfrac{1}{a}+\dfrac{1}{b}-\dfrac{1}{a+b} \blacksquare$
Proof 2
$(a+r)^2a+(b+r)^2b=(a+b)[(a+b-r)^2+ab]$
$\implies a^3+2a^2r+ar^2+b^3+2b^2r+br^2=(a+b)[a^2+b^2+3ab-2(a+b)r+r^2]$
$\implies 2(a^2+b^2)r+2(a+b)^2r=ab(b+3a)+ab(a+3b)=4ab(a+b)$
$\implies r=\dfrac{ab(a+b)}{a^2 + ab + b^2} \implies \dfrac{a+b}{r}=\dfrac{a^2 + ab + b^2}{ab} \implies \dfrac{a+b}{r}=\dfrac{(a+b)^2}{ab}-1$
$\implies \dfrac{1}{r}=\dfrac{a+b}{ab}-\dfrac{1}{a+b} \implies \dfrac{1}{r}=\dfrac{1}{a} + \dfrac{1}{b} - \dfrac{1}{a+b} \blacksquare$
11/06/2020
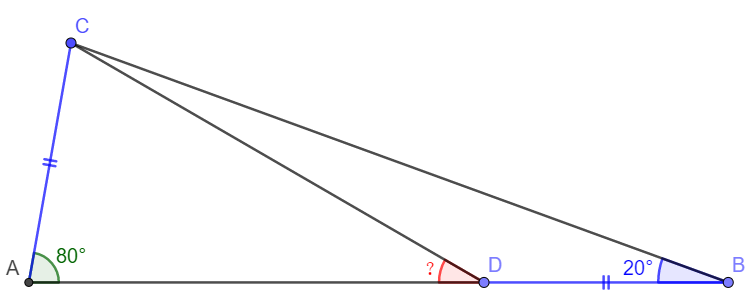
Solution:
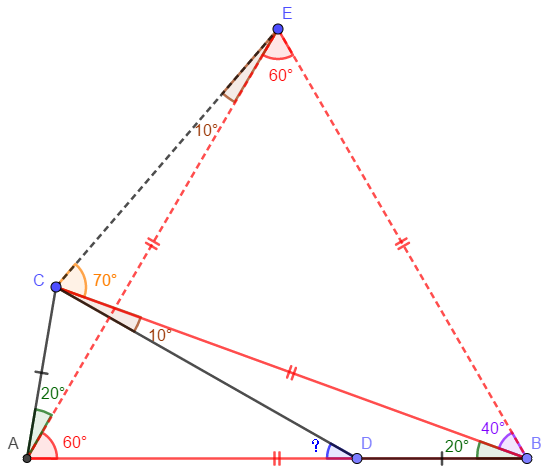
Make equilateral triangle $\triangle{ABE}$ with point $C$ and $E$ on the same side of $AB$. Easy to know :
$EA=AB=EB$, $\angle{CAE}=20^{\circ}$, $\triangle{CBE}=40^{\circ}$.
$CB=AB=EB, \angle{CBE}=40^{\circ} \implies \angle{CEB}=70^{\circ} \implies \angle{CEA}=10^{\circ}$
$\angle{CAE}=\angle{CBA}=20^{\circ}, EA=AB, AC=BD \implies \triangle{CAE} \cong \triangle{DBC}$
$ \implies \angle{DCB}=\angle{CEA}=10^{\circ} \implies \angle{CDA}=\angle{DCB} + \angle{CBD}=10^{\circ}+20^{\circ}=\bbox[1px, border: 1px solid black]{30^{\circ}}$
11/07/2020
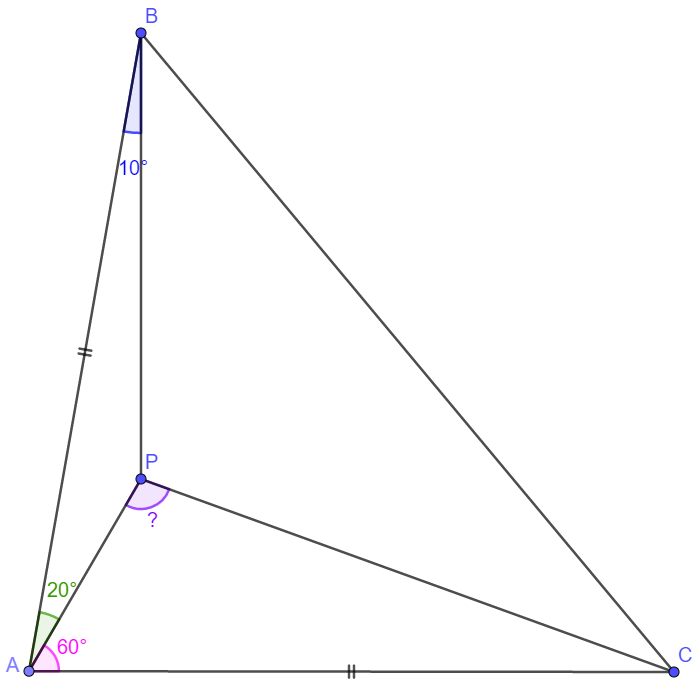
Solution:
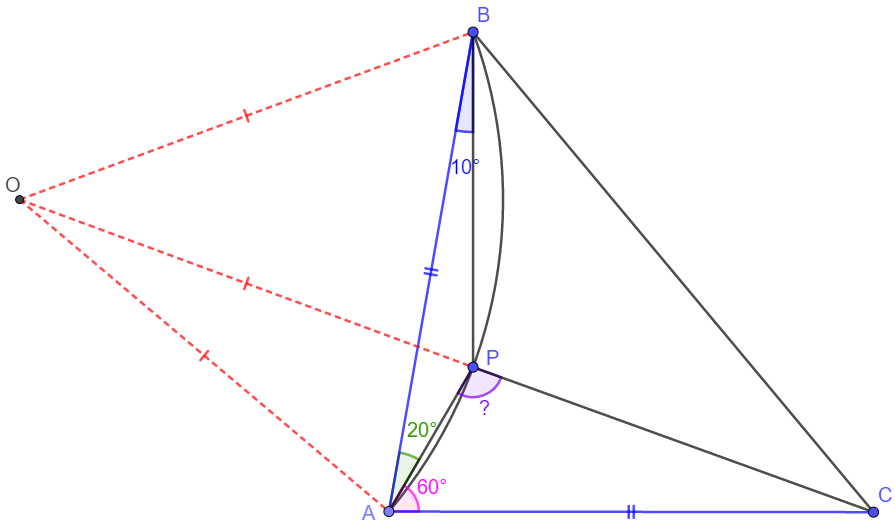
Let $O$ be the circumcenter of $ABP$. Then $\angle{AOP}=2 \angle{ABP}=20^{\circ}$ and
$\angle{BOP}=2 \angle{BAP}=40^{\circ} \implies \angle{AOB}=60^{\circ}$. This and $AO=BO$ shows that $\triangle{AOB}$ is equilateral.
So $\angle{OAB}=60^{\circ}$ and $AO=AB$. By assumption $AB=AC$, so $AO=AC$ and
$\angle{AOC}=90^{\circ}-\dfrac{1}{2} \angle{OAC}=90^{\circ}-\dfrac{1}{2} \cdot 140^{\circ}=20^{\circ}=\angle{AOP}$
Therefore, $O, P, C$ are collinear and we find
$\angle{APC}=\angle{OAP}+\angle{AOP}=80^{\circ}+20^{\circ}=\bbox[1px, border: 1px solid black]{100^{\circ}}$
11/08/2020
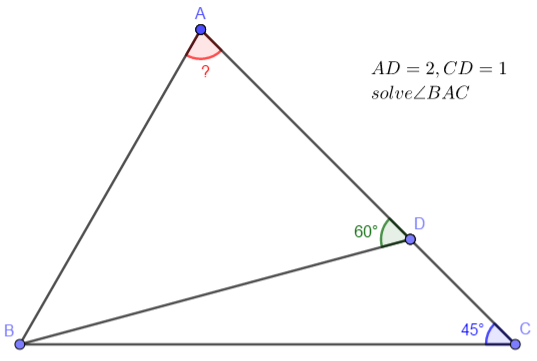
Solution:
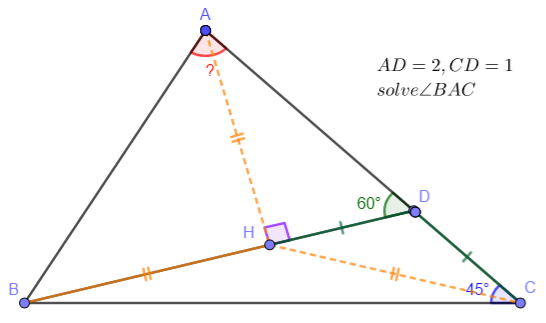
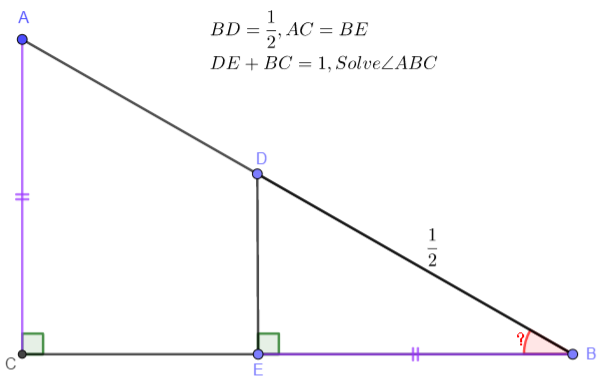
Solution:
$DE^2+BE^2=\dfrac{1}{4}$, $DE+BC=1$
$\dfrac{DE}{AC}=\dfrac{BE}{BC} \implies DE(1-DE)=BE^2$
$\implies DE=DE^2+BE^2=\dfrac{1}{4} \implies \angle{ABC}=\bbox[1px, border: 1px solid black]{30^{\circ}}$
11/09/2020
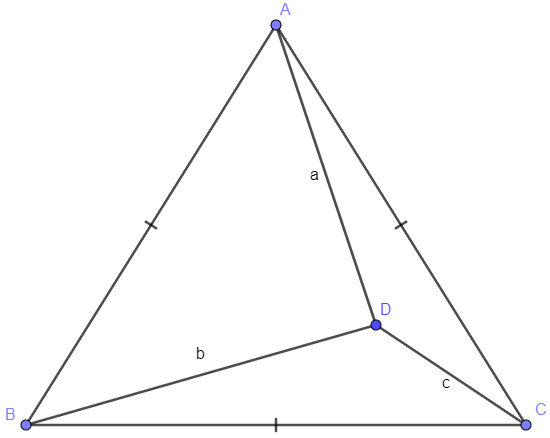
The distance from a point D inside equilateral triangle $\triangle{ABC}$ to the vertices are a, b and c respectively. Solve the area for $S_{\triangle{ABC}}$
Solution 1:
Rotate $\triangle{BDC}$ by $60^{\circ}$ to $\triangle{AEC}$ so we have $AE=b$.
Then $cos{\angle{ADE}}=\dfrac{a^2+c^2-b^2}{2ac}$,
$sin{\angle{ADE}}=\sqrt{1-\dfrac{(a^2+c^2-b^2)^2}{4a^2c^2}}$
$ = \dfrac{ \sqrt{(2ac+a^2+c^2-b^2)(2ac-a^2-c^2+b^2)} }{2ac} $
$ = \dfrac{\sqrt{(a+c+b)(a+c-b)(b+a-c)(b-a+c)}}{2ac} $
Then we know
$cos{\angle{ADC}}=cos(\angle{ADE}+60^{\circ})=cos{\angle{ADE}} \cdot cos60^{\circ} - sin{\angle{ADE}} \cdot sin{60^{\circ}}$
$=\dfrac{a^2+c^2-b^2}{4ac}-\dfrac{\sqrt{3(a+b+c)(a+b-c)(b+c-a)(c+a-b)}}{4ac}$
$=\dfrac{a^2+c^2-AC^2}{2ac}$
$ \implies AC^2=\dfrac{a^2+b^2+c^2}{2}+\dfrac{\sqrt{3(a+b+c)(a+b-c)(b+c-a)(c+a-b)}}{2} $
$ \implies S_{\triangle{ABC}}=\dfrac{\sqrt{3}}{4}AC^2 $
$=\bbox[1px, border: 1px solid black]{\dfrac{\sqrt{3}}{8}(a^2+b^2+c^2)+\dfrac{3}{8}\sqrt{(a+b+c)(a+b-c)(b+c-a)(c+a-b)}}$
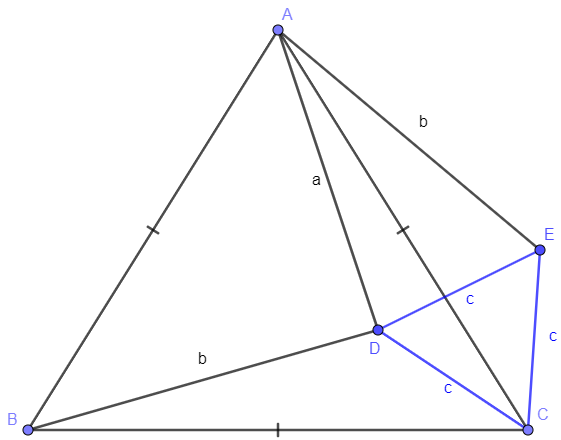
Solution 2:
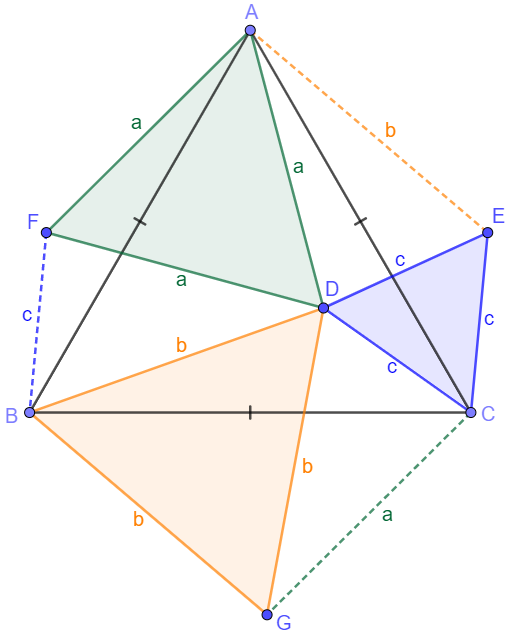
Rotate $\triangle{BDC}$ by $60^{\circ}$ to $\triangle{AEC}$ , $\triangle{CDA}$ by $60^{\circ}$ to $\triangle{BFA}$, $\triangle{ADB}$ by $60^{\circ}$ to $\triangle{CGB}$.
Easy to find that $CG=AF=a, AE=BG=b, BF=CE=c$.
So $S_{AFBGCE}=2 \cdot S_{\triangle{ABC}}=3 \cdot S_{\triangle{CDG}} + S_{\triangle{CDE}} + S_{\triangle{BDG}} + S_{\triangle{ADF}}$
According to Heron’s formula :
$S_{\triangle{CDG}}=\dfrac{\sqrt{(a+b+c)(a+b-c)(b+c-a)(c+a-b)}}{4}$
And we know
$S_{\triangle{CDE}}=\dfrac{\sqrt{3}}{4} c^2$, $S_{\triangle{BDG}}=\dfrac{\sqrt{3}}{4} b^2$, $S_{\triangle{ADF}}=\dfrac{\sqrt{3}}{4} a^2$
So we have
$S_{\triangle{ABC}}=\bbox[1px, border: 1px solid black]{\dfrac{\sqrt{3}}{8}(a^2+b^2+c^2)+\dfrac{3}{8}\sqrt{(a+b+c)(a+b-c)(b+c-a)(c+a-b)}}$
11/10/2020
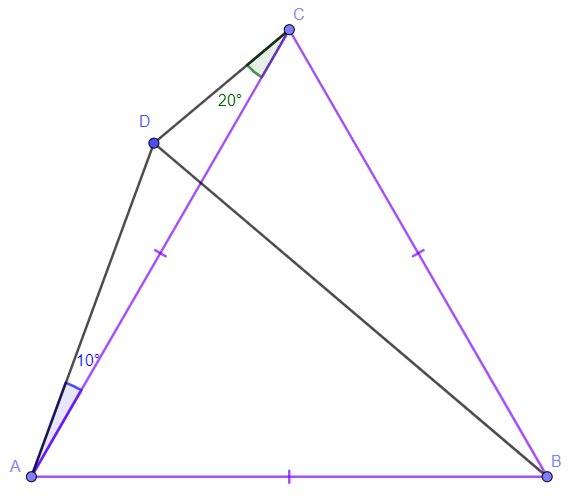
$\triangle{ABC}$ is equilateral. Point $D$ is outside $\triangle{ABC}$ and $\angle{DAC}=10^{\circ}$, $\angle{DCA}=20^{\circ}$. Prove $BC=BD$
Make circumcircle of $\triangle{ACD}$, suppose the center of the circle is $B’$. Then we know
-
Point $D$ and $B’$ cannot be on the same side of line $AC$, so $B’$ and $B$ are on the same side of line $AC$.
-
$AB’=DB’=CB’, \angle{AB’C}=\angle{AB’D} + \angle{DB’C}\ = 2 \cdot \angle{ACD} + 2 \cdot \angle{DAC} = 40^{\circ} + 20^{\circ} = 60^{\circ}$ So $\triangle{AB’C}$ is also equilateral.
From 1 and 2 we know $B$ is the same as $B’$, then $BC=BD$. $\blacksquare$
11/12/2020
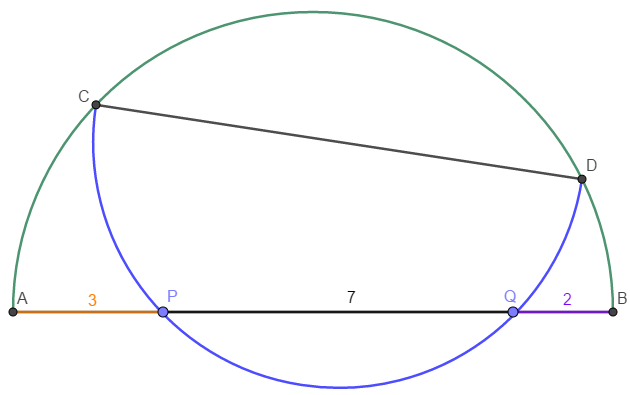
A semicircle is constructed on line segment $AB$. Another semicircle is constructed on chord $CD$, intersecting $AB$ at $P$ and $Q$. If $AP = 3$,$PQ = 7$, and $QB = 2$, then find the length $CD$.
Solution 1:
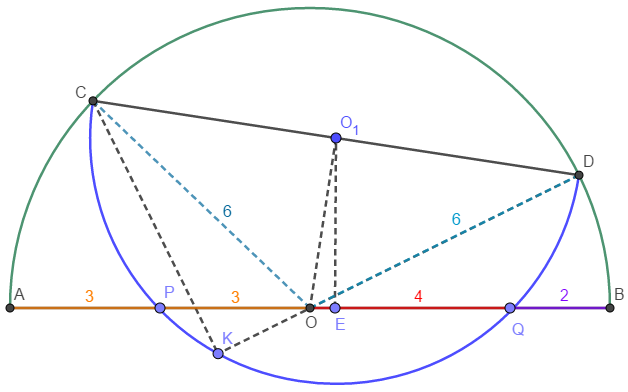
$ \triangle{POK} \sim \triangle{DOQ}, PO=3, DO=6, OQ=4$ $ \implies KO = 2 \implies CD= \sqrt{6^2+8^2-2^2}=\bbox[1px, border: 1px solid black]{\sqrt{96}} $
Solution 2:
$OE=\dfrac{1}{2}, PE=\dfrac{7}{2},O_1E^2+OE^2=OO_1^2$, $O_1E^2 + PE^2 = PO_1^2 = CO_1^2=OO_1^2-\dfrac{1}{4}+\dfrac{49}{4}=OO_1^2 + 12$
$OO_1^2 + CO_1^2 = CO^2 = 6^2 \implies CO_1^2 = 24 \implies CD = \bbox[1px, border: 1px solid black]{2\sqrt{24}=\sqrt{96}}$
11/13/2020
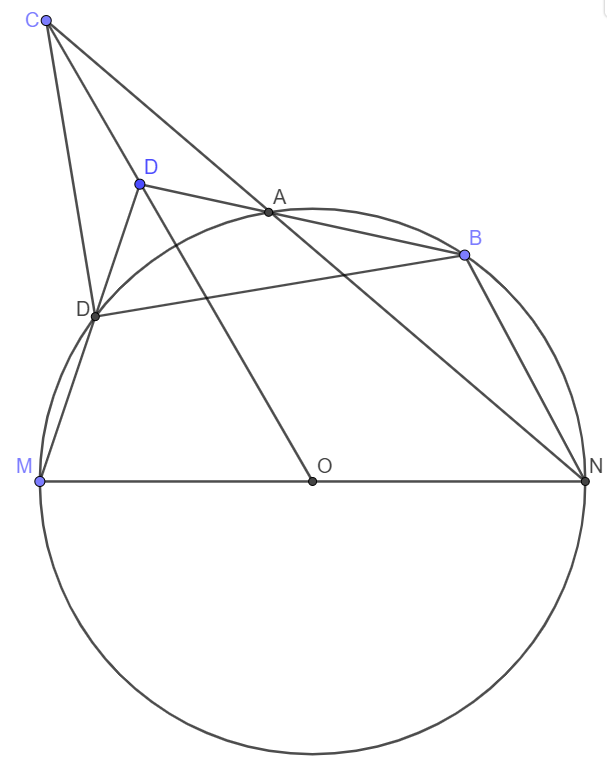
Point D is outside of circle O with diameter MN. From D make two lines DM and DB with points D, A and B on the circle O. Extend OD and NA to intersect at point C. Prove that $CD \perp DB$.
11/14/2020
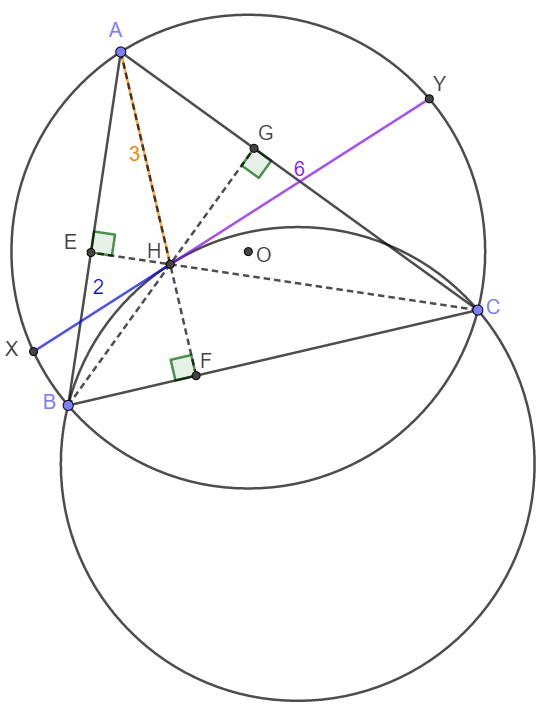
Let $\triangle{ABC}$ be an acute triangle with circumcircle $\omega$, and let $H$ be the intersection of the altitudes of $\triangle{ABC}$. Suppose the tangent to the circumcircle of $\triangle{HBC}$ at $H$ intersects $\omega$ at points $X$ and $Y$ with $HA=3$, $HX=2$, and $HY=6$. the area of $\triangle{ABC}$ can be written in the form $m\sqrt{n}$, where $m$ and $n$ are positive integers, and $n$ is not divisible by the square of any prime. Find $m+n$.
11/15/2020
Find all primes $p$ to make $p^3-2p+4$ is a perfect square.
Solution:
If $q=3k+1$ or $3k-1$, then $q^2=1(mod3)$ But if $p=3k+1$, $p^3-2p+4=0 (mod3)$, if $p=3k-1$, $p^3-2p+4=2 (mod3)$ only when $p=3k$, $p^3-2p+4=1 (mod3)$ and $p$ must be prime, so $\bbox[1px, border: 1px solid black]{k=1, p=3}$ is the only one.
11/16/2020
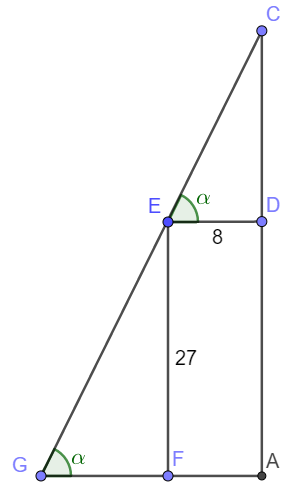
A scale model of a building is 8 inches wide and 27 inches tall. It is placed against a wall. What is the length of the shortest pole that will reach the wall above it from the level ground?
Solution 1:
Use trigonometry it is easier to get $CG = \dfrac{8}{cos \alpha} + \dfrac{27}{sin \alpha}$, it gets minimum value when
$\dfrac{8 sin \alpha}{cos^2 \alpha}- \dfrac{27 cos \alpha}{sin^2 \alpha}=0 \implies tan \alpha=\dfrac{3}{2} \implies CG_{min}=\bbox[1px, border: 1px solid black]{13\sqrt{13}}$
Note: to avoid trigonometrical approach, it would be a hard work to solve this problem, seems.
Solution 2:
Get another solution based on another problem on 11/30/2020:
Suppose $AF=a, AD=b, FG=x, CD=y, CG=l$
$\dfrac{y}{a}=\dfrac{b}{x} \implies xy=ab$
$l^2=(a+x)^2+(b+y)^2=(a+x)^2+(b+\dfrac{ab}{x})^2$
$l^2$ gets minimum value when
$2(a+x)+2(b+\dfrac{ab}{x})(-\dfrac{ab}{x^2})=0$
$\implies (x^3-ab^2)(x+a)=0$
$\implies x=\sqrt[3]{ab^2}, y=\sqrt[3]{a^2b}$
$\implies l_{min}=\bbox[1px, border: 1px solid black]{\sqrt{a^2+3a\sqrt[3]{ab^2}+3b\sqrt[3]{a^2b}+b^2}}$
11/17/2020
How many sequences of integers $\{a_1, a_2, …, a_7\}$ are there for which $-1 \le a_i \le 1$ for every $i$, and $a_1a_2+a_2a_3+a_3a_4+a_4a_5+a_5a_6+a_6a_7 = 4$?
11/18/2020
There are 12 students in a classroom: 6 of them are Democrats and 6 of them are Republicans. Every hour the students are randomly separated into four groups of three for political debates. If a group contains students from both parties, the minority in the group will change his/her political alignment to that of the majority at the end of the debate. What is the expected amount of time needed for all 12 students to have the same political alignment, in hours? (HMMT November 2017 Team Round Problem 7)
Solution:
11/22/2020
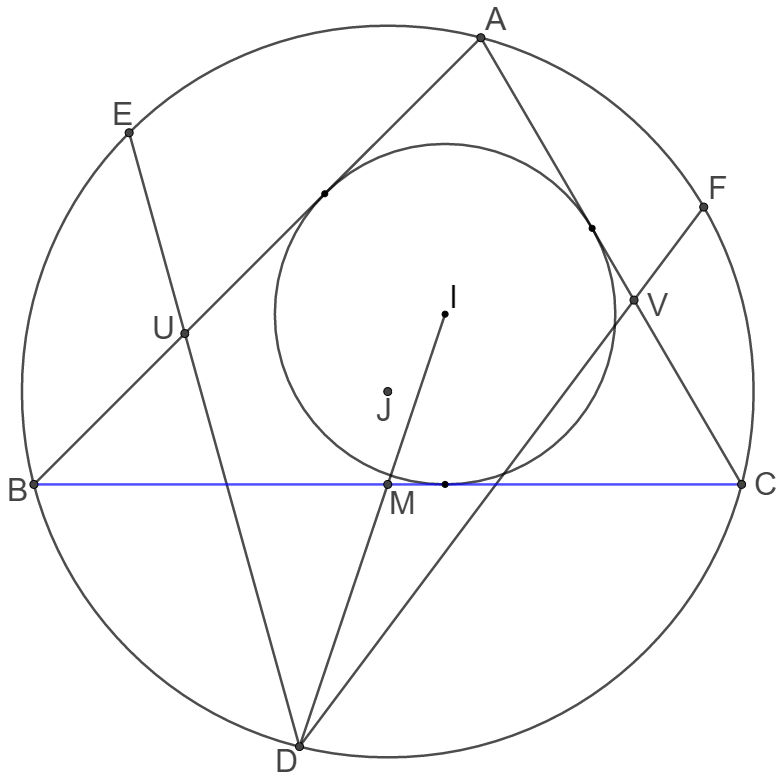
Point $I$ is the incenter of $\triangle{ABC}$ and point $M$ bisects side $BC$. Extend line IM and intersects circumcircle of $\triangle{ABC}$ at point $D$. Point $E$ and $F$ bisects the arc $\overset{\large\frown}{AB}$ and $\overset{\large\frown}{BC}$. Line $DE$ intersects $AB$ at point $U$, Line $DF$ intersects $BC$ at point $V$. Prove: $BU=CV$
Proof:
Point $E$ bisects the arc $\overset{\large\frown}{AB}$
$ \implies \angle{EBU}=\angle{BDE} \implies \triangle{EBU} \sim \triangle{EBD}$
$ \implies \dfrac{BU}{BE}=\dfrac{BD}{DE}\implies BU=\dfrac{BD \cdot BE}{DE}$
Point $F$ bisects the arc $\overset{\large\frown}{BC}$
$\implies \dfrac{CV}{CF}=\dfrac{CD}{DF} \implies CV=\dfrac{CD \cdot CF}{DF}$
$sin \angle{BDF} = sin \angle{BCF}, \cdot sin \angle{CBE} = sin \angle{CDE}$
$ \implies \dfrac{BD \cdot BE \cdot DF}{CD \cdot DE \cdot CF} = \dfrac{BD \cdot DF \cdot sin \angle{BDF} \cdot BE \cdot BC \cdot sin \angle{CBE}}{CD \cdot DE \cdot sin \angle{CDE} \cdot CF \cdot BC \cdot sin \angle{BCF}}$
$ = \dfrac{S_{\triangle{BDF}}}{S_{\triangle{CDE}}}\dfrac{S_{\triangle{BCE}}}{S_{\triangle{BCF}}}$
$S_{\triangle{BCE}}=2S_{\triangle{CEM}}=2\dfrac{IM}{ID}S_{\triangle{CDE}}$
$S_{\triangle{BCF}}=2S_{\triangle{BFM}}=2\dfrac{IM}{ID} S_{\triangle{BDF}}$
$\implies \dfrac{BD \cdot BE \cdot DF}{BD \cdot DF \cdot BE \cdot BC}=1 \implies BU=CV \blacksquare$
11/23/2020
In a single-elimination tournament consisting of $2^9=512$ teams, there is a strict ordering on the skill levels of the teams, but Joy does not know that ordering. The teams are randomly put into a bracket and they play out the tournament, where the better team always beats the worse team. Joy is then given the results of all $511$ matches and must write a list of teams such that she can guarantee that the third-best team is on the list. What is the minimum possible length of Joy’s list$\text{?}$ (Shared by Brady from HMMT Guts Test November 2020)
Solution:
After understanding the model, easy to know that, checking the result of all $511$ matches, the only team who won 9 matches is the first team in the skill level list.
The second best team must be one of those teams who lost to the first team - because only the best team can win it. There are 9 teams in this set.
The third best team has two situations:
- It could be one of the teams who lost to the first team - it could be in the 9-team-set.
- Or, it could be one of the teams who lost to any team from the 9-team-set.
Check the teams in the 9-team-set:
- There is a team lost in the 1st round, and 0 team lost to it.
- There is a team lost in the 2nd round, and 1 team lost to it.
- There is a team lost in the 3rd round, and 2 teams lost to it.
- …
- There is a team lost in the 9th round, and 8 teams lost to it.
So totally there are $1+2+…+8=36$ teams lost to any team from the 9-team-set.
To include two situations for the third best team, we need the list length no shorter than $9 + 36 = \bbox[1px, border: 1px solid black]{45}$ to guarantee that the third best team in it.
11/24/2020
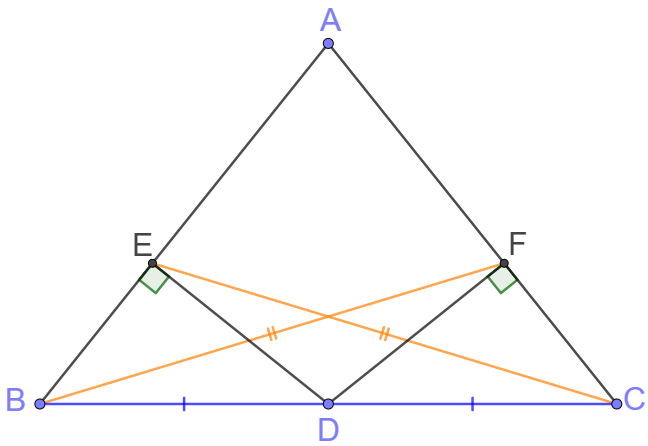
Point $D$ bisects side $BC$ in $\triangle{ABC}$ and $DE \perp AB, DF \perp AC, BF=CE$ , prove: $AB=AC$
Proof:
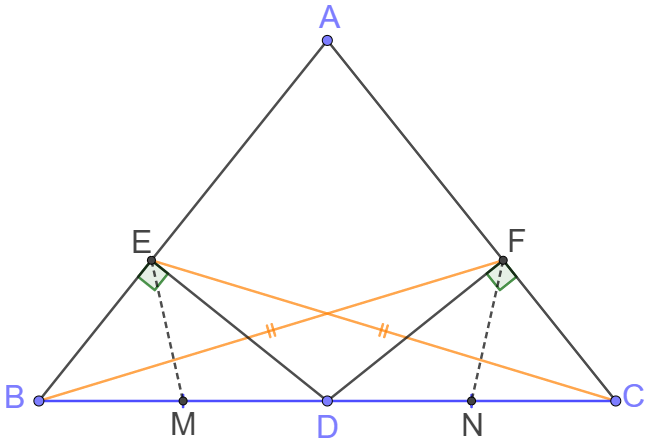
Let point $M$ and $N$ bisects $BD$ and $DC$ respectively.
$BD=DC=2ME=2NF \implies ME=NF, CM=BN$
and we already know $BF=CE$, so
$\triangle{BNF} \cong \triangle{CME} \implies \angle{ECB}=\angle{FBC}$
so $\triangle{ECB} \cong \triangle{FBC} \implies \angle{EBC}=\angle{FCB} \blacksquare$
11/25/2020
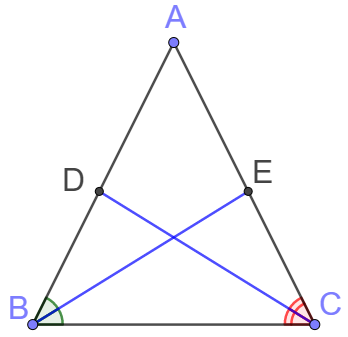
$CD$ and $BE$ are angle bisectors of $\triangle{ABC}$ and $CD=BE$. Prove $AB=AC.$
Proof 1:
Let $AC=b, AB=c, BC=a, CD=e, BE=f$
From Length of Angle Bisector:
$e^2=\dfrac{ab}{(a+b)^2}((a+b)^2-c^2)$
$f^2=\dfrac{ac}{(a+c)^2}((a+c)^2-b^2)$
$e=f \implies b-\dfrac{bc^2}{(a+b)^2}=c-\dfrac{b^2c}{(a+c)^2}$
$\implies (b-c)+bc\dfrac{b(a+b)^2-c(a+c)^2}{(a+b)^2(a+c)^2}=0$
$\implies (b-c)+bc\dfrac{a^2(b-c)+2a(b^2-c^2)+(b^3-c^3)}{(a+b)^2(a+c)^2}=0$
$\implies (b-c)(1+bc\dfrac{a^2+2ab+2ac+a^2+ab+c^2}{(a+b)^2(a+c)^2})=0$
$\implies (b-c)\dfrac{(a+b)^2(a+c)^2+bc[(a+b+c)^2-ab]}{(a+b)^2(a+c)^2}=0$
$a+b+c>a, a+b+c>b \implies (a+b+c)^2-ab>0$
$\implies b-c=0 \implies AB=AC \blacksquare$
Proof 2:
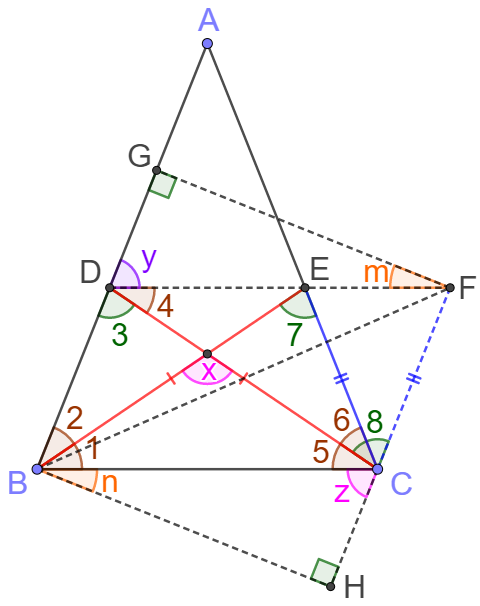
Draw $\angle{DCF}=\angle{8}=\angle{BEC}=\angle{7}$ and make $CE=CF$. Then connect $D$ and $F$.
$CD=BE, CE=CF, \angle{7}=\angle{8} \implies \triangle{BCE} \cong \triangle{DFC}$
$\implies BC=DF, \angle{1}=\angle{4}$
$\angle{x}=\angle{2}+\angle{3}=\angle{1}+\angle{3}=\angle{4}+\angle{3}=\angle{6}+\angle{7}=\angle{5}+\angle{7}=\angle{5}+\angle{8}$
$\implies \angle{4}+\angle{3}=\angle{5}+\angle{8} \implies \angle{y}=\angle{z}$
Draw $FG \perp AB, BH \perp CF$, $BC=DF,\angle{y}=\angle{z} \implies \triangle{DFG} \cong \triangle{BCH}$
$\implies DG=CH, FG=BH \implies \triangle{BFG} \cong \triangle{BFH}$
$\implies BHFG \text{ is a parallelogram } \implies \angle{m}=\angle{n}$
$\implies \angle{DBC}=\angle{DFC}=\angle{ECB}\blacksquare$
Proof 3:
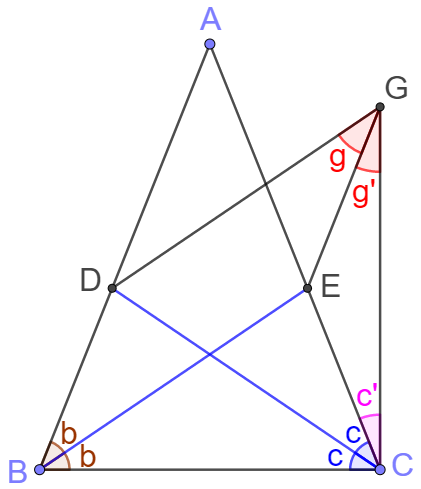
Assume $\triangle{ABC}$ is not isosceles. Let $\angle{ABC} > \angle{ACB}$.
$CD=BE, BC=BC, CE>BD$ (if two triangles have two pairs of corresponding sides congruent and their included angles are not congruent, then the greater third side is opposite the greater included angle).
Through point $E$, construct $EG \parallel AB, DG \parallel BE$, so $BDGE$ is a parallelogram
$\implies BE=DG, CD=BE \implies CD=DG$
$ \implies \angle{(g+g’)}=\angle{(c+c’)}, \angle{g}=\angle{b}$
$\implies \angle{b+g’}=\angle{c+c’}$
$\angle{b}>\angle{c} \implies \angle{g’}<\angle{c’} \implies CE < EG \implies CE < BD$
The assumption of the inequality of $\angle{ABC}$ and $\angle{ACB}$ leads to two contradictory results: $CE>BD$ and $CE<BD$.
Therefore, $\triangle{ABC}$ is isosceles.$\blacksquare$
11/27/2020
A sphere is centered at a point with integer coordinates and passes through the three points $(2,0,0), (0,4,0), (0,0,6)$, but not the origin $(0,0,0)$. If $r$ is the smallest possible radius of the sphere, compute $r^2$. (HMMT General, November 2020)
Solution:
Suppose the center of the sphere is $(x_0, y_0, z_0)$
$(x_0-2)^2+y_0^2+z_0^2=r^2$
$x_0^2+(y_0-4)^2+z_0^2=r^2$
$x_0^2+y_0^2+(z_0-6)^2=r^2$
$x_0^2-4x_0+4+y_0^2+z_0^2=x_0^2+y_0^2-8y_0+16+z_0^2=x_0^2+y_0^2+z_0^2-12z_0+36$
$\implies x_0=2y_0-3=3z_0-8 \implies x_0=3z_0-8, y_0=\dfrac{3z_0-5}{2}$, $z_0$ is odd
$\implies (3z_0-8)^2+(\dfrac{3z_0-5}{2})^2+(z_0-4)^2=r^2$
$\implies 49z_0^2-270z_0+425=4r^2$
If $z_0 \in \mathbb{R}$, when $z_0=\dfrac{270}{98}$, $4r^2$ get minimum value.
The closest odd integer to $\dfrac{270}{98}$ is
$z_0=3 \implies x_0=1, y_0=2 \implies r^2=14$
but $x_0^2+y_0^2+z_0^2=14=r^2$ so this is not solution.
The second closest odd integer to $\dfrac{270}{98}$ is
$z_0=1 \implies x_0=-5, y_0=-1 \implies r^2=51$
and $z_0^2+y_0^2+z_0^2=27 \ne r^2$
So the solution is $r^2=\bbox[1px, border: 1px solid black]{51}$.
11/30/2020
Solve over the integers: $615+x^2=2^y$
Solution:
Easy to see $x \equiv 1 \text{ mod 2}$. The last digit of $x^2$ could be $1,5,9$ thus the last digit of $615+x^2$ could be $0, 4, 6$, but the last digit of $2^y$ could be $2, 4, 6, 8$ so the common subset of the last digit of $2^y$ is $4, 6$, and this means $y \equiv 0 \text{ mod 2}$.
Suppose $y=2k$, then $615=2^{2k}-x^2=(2^k+x)(2^k-x)$. We know that $615=41 \times 5 \times 3$, so \(\begin{align*} &\begin{cases} 2^k+x=41\\ 2^k-x=15 \end{cases} \implies 2^k=28 \implies \text{no integer solution},\\ &\begin{cases} 2^k+x=123\\ 2^k-x=5 \end{cases} \implies 2^k=64 \implies k=6, x=59, y=12 \end{align*}\\ \begin{cases} 2^k+x=205\\ 2^k-x=3 \end{cases} \implies 2^k=104 \implies \text{no integer solution}\\ \begin{cases} 2^k+x=615\\ 2^k-x=1 \end{cases} \implies 2^k=308 \implies \text{ no integer solution}\)
So the answer is $\bbox[1px, border: 1px solid black]{x=59, y=12}$
11/30/2020
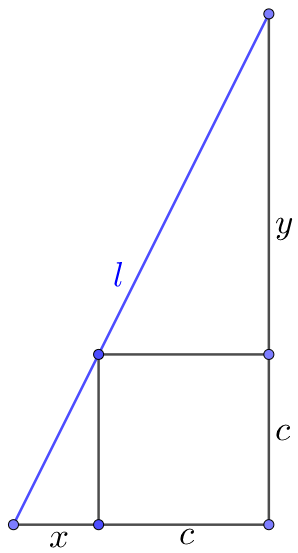
$l$ and $c$ are known. Find $x$ and $y$. This problem seems similar to a previous one.
Solution:
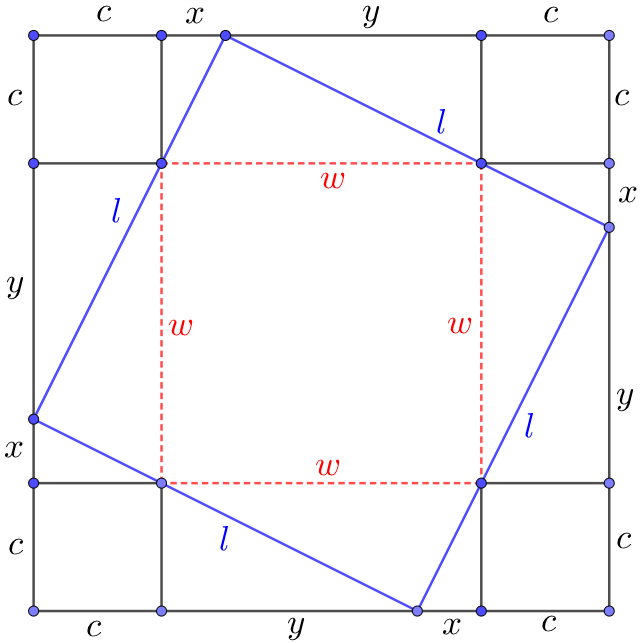
$\dfrac{y}{c}=\dfrac{c}{x} \implies xy=c^2$
$\implies l=\sqrt{xy+x^2}+\sqrt{xy+y^2}$
$w=x+y \implies l=\sqrt{xw}+\sqrt{yw}=\sqrt{w}(\sqrt{x}+\sqrt{y})$
$\implies l^2=w(x+y+2\sqrt{xy})=w(w+2c)$
$w^2+2cw-l^2=0 \implies w=\dfrac{-2c+\sqrt{4c^2+4l^2}}{2}=\sqrt{c^2+l^2}-c$
So $x$,$y$ are roots of $t^2-(\sqrt{c^2+l^2}-c)t+c^2=0$:
$\implies x,y=\dfrac{\sqrt{c^2+l^2}-c \pm \sqrt{l^2-2c^2-2c\sqrt{c^2+l^2}}}{2}$
$\implies y=\bbox[1px, border: 1px solid black]{\dfrac{\sqrt{c^2+l^2}-c+\sqrt{l^2-2c^2-2c\sqrt{c^2+l^2}}}{2}}$